In diesem Thema
Mittelwert
Ein häufig verwendetes Maß für das Zentrum einer Gruppe von Zahlen. Der Mittelwert wird auch als Durchschnitt bezeichnet. Es handelt sich um die Summe aller Beobachtungen dividiert durch die Anzahl der (nicht fehlenden) Beobachtungen.
Formel
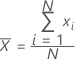
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
| N | Anzahl der nicht fehlenden Beobachtungen |
Standardfehler des Mittelwerts (SE des Mittelwerts)
Der Standardfehler des Mittelwerts wird berechnet, indem die Standardabweichung durch die Quadratwurzel des Stichprobenumfangs dividiert wird.
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| s | Standardabweichung der Stichprobe |
| N | Anzahl der nicht fehlenden Beobachtungen |
Standardabweichung (StdAbw)
Die Standardabweichung der Stichprobe bietet ein Maß für die Streubreite der Daten. Sie entspricht der Quadratwurzel der Varianz der Stichprobe.
Formel
 , dann ist die Standardabweichung der Stichprobe:
, dann ist die Standardabweichung der Stichprobe:
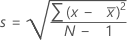
Notation
| Begriff | Beschreibung |
|---|---|
| x i | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
Varianz
Die Varianz ist ein Maß der Streuung der Daten um ihren Mittelpunkt. Die Varianz ist gleich dem Quadrat der Standardabweichung.
Formel
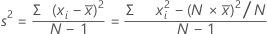
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
Variationskoeffizient (KoefVar)
Der Variationskoeffizient ist ein als Prozentsatz ausgedrücktes Maß für die relative Streuung.
Formel

Minitab berechnet ihn wie folgt:

Notation
| Begriff | Beschreibung |
|---|---|
| s | Standardabweichung der Stichprobe |
 | Mittelwert der Beobachtungen |
1. Quartil (Q1)
25 % Ihrer Stichprobenbeobachtungen sind kleiner oder gleich dem Wert des 1. Quartils. Daher wird das 1. Quartil auch als das 25. Perzentil bezeichnet.
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| y | auf ganze Zahl abgeschnittener Wert von w |
| w | 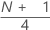 |
| z | abgeschnittener Nachkommaanteil von w |
| xj | j-te Beobachtung in der Liste von Stichprobendaten, von der kleinsten zur größten geordnet |
Hinweis
Wenn w eine ganze Zahl ist: y = w, z = 0 und Q1 = xy.
Median
Der Stichproben-Median liegt in der Mitte der Daten: Mindestens die Hälfte der Beobachtungen sind kleiner oder gleich und mindestens die Hälfte sind größer oder gleich dem Stichproben-Median.
Angenommen, eine Spalte enthält N Werte. Um den Median zu berechnen, ordnen Sie die Datenwerte zunächst vom kleinsten zum größten an. Wenn N eine ungerade Zahl ist, handelt es sich bei dem Stichproben-Median um den Wert in der Mitte. Wenn N eine gerade Zahl ist, handelt es sich bei dem Stichproben-Median um den Durchschnitt der beiden mittleren Werte.
Beispiel: Wenn N = 5 und die Daten x1, x2, x3, x4 und x5 vorliegen, ist der Median = x3.
Wenn N = 6 und die geordneten Daten x1, x2, x3, x4, x5 und x6 vorliegen:

wobei x3 und x4 die dritte und vierte Beobachtung sind.
3. Quartil (Q3)
75 % Ihrer Stichprobenbeobachtungen sind kleiner oder gleich dem Wert des dritten Quartils. Daher wird das dritte Quartil auch als das 75. Perzentil bezeichnet.
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| y | auf ganze Zahl abgeschnittener Wert von w |
| w |
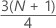 |
| z | abgeschnittener Nachkommaanteil von w |
| xj | j-te Beobachtung in der Liste von Stichprobendaten, von der kleinsten zur größten geordnet |
Hinweis
Wenn w eine ganze Zahl ist: y = w, z = 0 und Q3 = xy.
Interquartilbereich (IQR)
Der Interquartilbereich entspricht dem dritten Quartil minus dem ersten Quartil.
Getrimmtes Mittel (TrMW)
Minitab berechnet das getrimmte Mittel, indem die kleinsten 5 % und die größten 5 % der Werte (auf die nächste ganze Zahl gerundet) entfernt werden und dann der Mittelwert der verbleibenden Werte berechnet wird.
Summe
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
Minimum
Der kleinste Wert im Datensatz.
Maximum
Der größte Wert in Ihrem Datensatz.
Spannweite
Die Spannweite wird als Differenz zwischen dem größten und dem kleinsten Datenwert berechnet.
R = Maximum – Minimum
Summe der Quadrate
Minitab quadriert jeden Wert der Spalte und berechnet dann die Summe dieser quadrierten Werte.
Formel
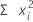
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
Schiefe
Schiefe ist ein Maß für Asymmetrie. Ein negativer Wert gibt eine Schiefe nach links an, und ein positiver Wert gibt eine Schiefe nach rechts an. Ein Nullwert deutet nicht unbedingt auf Symmetrie hin.
Formel
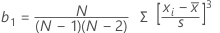
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
| s | Standardabweichung der Stichprobe |
Kurtosis
Die Kurtosis ist ein Maß dafür, wie weit eine Verteilung von der Normalverteilung abweicht. Ein positiver Wert deutet in der Regel darauf hin, dass sich die Verteilung durch eine steilere Wölbung als die Normalverteilung auszeichnet. Ein negativer Wert deutet darauf hin, dass die Verteilung eine flachere Wölbung als die Normalverteilung aufweist.
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
| s | Standardabweichung der Stichprobe |
MSSD (Mittel der quadrierten sukzessiven Differenzen)
Minitab berechnet die Hälfte des Mittels der quadrierten sukzessiven Differenzen (MSSD) einer Gruppe von Zahlen. Die sukzessiven Differenzen werden quadriert und summiert. Anschließend dividiert Minitab den Wert durch 2 und berechnet den Durchschnitt.
Formel
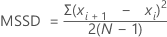
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
N nicht fehlend (N)
Die Anzahl der nicht fehlenden Werte in der Stichprobe.
N fehlend (N*)
Die Anzahl der fehlenden Werte in der Stichprobe. Die Anzahl der fehlenden Werte bezieht sich auf Zellen, die das Symbol für fehlende Werte * enthalten.
N gesamt (Gesamtanzahl)
Die Gesamtanzahl der Beobachtungen in der Spalte.
Prozent
Minitab berechnet, welcher Prozentsatz des Ganzen von jeder Gruppe dargestellt wird.
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| ni | Anzahl der Beobachtungen in der i-ten Gruppe |
| N | Anzahl der nicht fehlenden Beobachtungen |
Kumuliert in Prozent (Kum%)
Minitab berechnet den von jeder Gruppe dargestellten kumulierten Prozentsatz.
Formel
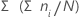
Notation
| Begriff | Beschreibung |
|---|---|
| ni | Anzahl der Beobachtungen in der i-ten Gruppe |
| N | Anzahl der nicht fehlenden Beobachtungen |
