In diesem Thema
Mittelwert
Der Mittelwert ist der Durchschnitt der Daten; hierbei handelt es sich um die Summe aller Beobachtungen dividiert durch die Anzahl der Beobachtungen.
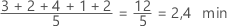
Interpretation
Verwenden Sie den Mittelwert, um die Stichprobe mit einem einzelnen Wert zu beschreiben, der das Zentrum der Daten darstellt. In vielen statistischen Analysen wird der Mittelwert als Standardmaß für die Lage der Datenverteilung verwendet.
Symmetrisch
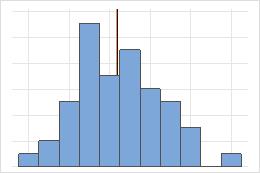
Nicht symmetrisch
Bei der symmetrischen Verteilung ähneln sich der Mittelwert (blaue Linie) und der Median (orangefarbene Linie) so sehr, dass die Linien nicht ohne weiteres unterschieden werden können. Die nicht symmetrische Verteilung ist jedoch rechtsschief.
SE des Mittelwerts
Der Standardfehler des Mittelwerts (SE des Mittelwerts) schätzt die Streuung zwischen den Stichprobenmittelwerten, die Sie erhalten würden, wenn Sie wiederholt Stichproben aus derselben Grundgesamtheit ziehen. Mit dem Standardfehler des Mittelwerts wird die Streuung zwischen Stichproben geschätzt, während mit der Standardabweichung die Streuung innerhalb einer Stichprobe gemessen wird.
Angenommen bei einer Zufallsstichprobe von 312 Lieferungen beträgt die mittlere Lieferzeit 3,80 Tage, mit einer Standardabweichung von 1,43 Tagen. Diese Werte ergeben einen Standardfehler des Mittelwerts von 0,08 Tagen (1,43 dividiert durch die Quadratwurzel von 312). Würden Sie mehrere zufällig ausgewählte Stichproben gleicher Größe aus derselben Grundgesamtheit ziehen, betrüge die Standardabweichung der verschiedenen Stichprobenmittelwerte etwa 0,08 Tage.
Interpretation
Verwenden Sie den Standardfehler des Mittelwerts, um zu bestimmen, wie präzise der Mittelwert der Stichprobe den Mittelwert der Grundgesamtheit schätzt.
Ein kleinerer Wert des Standardfehlers des Mittelwerts zeigt einen präziseren Schätzwert für den Mittelwert der Grundgesamtheit an. Im Allgemeinen ergibt eine größere Standardabweichung einen größeren Standardfehler des Mittelwerts und einen weniger präzisen Schätzwert für den Mittelwert der Grundgesamtheit. Ein größerer Stichprobenumfang ergibt einen kleineren Standardfehler des Mittelwerts und einen präziseren Schätzwert für den Mittelwert der Grundgesamtheit.
In Minitab wird mit dem Standardfehler des Mittelwerts das Konfidenzintervall berechnet.
StdAbw
Die Standardabweichung ist das am häufigsten verwendete Maß für die Streuung bzw. die Streubreite der Daten um den Mittelwert. Die Standardabweichung einer Grundgesamtheit wird häufig mit dem Zeichen σ (Sigma) angegeben, während mit s die Standardabweichung einer Stichprobe dargestellt wird. Eine zufällige oder natürliche Streuung eines Prozesses wird häufig auch als Rauschen bezeichnet.
Da die Standardabweichung in der gleichen Einheit wie die Daten angegeben wird, lässt sie sich in der Regel einfacher als die Varianz interpretieren.
Interpretation
Verwenden Sie die Standardabweichung, um die Streubreite der Daten um den Mittelwert zu ermitteln. Ein höherer Wert der Standardabweichung verweist auf eine größere Streubreite der Daten. Eine Faustregel für die Normalverteilung besagt, dass etwa 68 % der Werte innerhalb einer Standardabweichung vom Mittelwert, 95 % der Werte innerhalb zwei Standardabweichungen und 99,7 % der Werte innerhalb drei Standardabweichungen liegen.

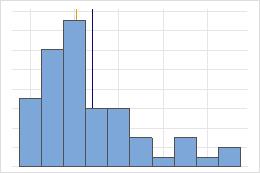
Krankenhaus 1
Krankenhaus 2
Zeit bis zur Entlassung in Krankenhäusern
Verwaltungsangestellte zeichnen die Zeit bis zur Entlassung von Patienten auf, die in der Notaufnahme zweier Krankenhäuser behandelt werden. Obwohl die durchschnittliche Zeit bis zur Entlassung in etwa identisch ist (35 Minuten), weichen die Standardabweichungen signifikant voneinander ab. Die Standardabweichung für Krankenhaus 1 beträgt etwa 6. Im Durchschnitt weicht die Zeit bis zur Entlassung eines Patienten um etwa 6 Minuten vom Mittelwert (gestrichelte Linie) ab. Die Standardabweichung für Krankenhaus 2 beträgt etwa 20. Im Durchschnitt weicht die Zeit bis zur Entlassung eines Patienten um ca. 20 Minuten vom Mittelwert (gestrichelte Linie) ab.
Varianz
Die Varianz ist ein Maß der Streuung der Daten um ihren Mittelpunkt. Die Varianz ist gleich dem Quadrat der Standardabweichung.
Interpretation
Je größer die Varianz, desto größer ist die Streubreite der Daten.
Da die Varianz (σ2) einen quadrierten Betrag darstellt, sind ihre Einheiten ebenfalls quadriert, was ihre praktische Verwendung möglicherweise erschwert. Die Standardabweichung lässt sich in der Regel einfacher interpretieren, da sie in den gleichen Einheiten wie die Daten vorliegt. Angenommen, eine Stichprobe von Wartezeiten an einer Bushaltestelle weist einen Mittelwert von 15 Minuten und eine Varianz von 9 min2 auf. Da die Varianz nicht in der gleichen Einheit wie die Daten angegeben wird, wird sie oft mit ihrer Quadratwurzel angezeigt, der Standardabweichung. Eine Varianz von 9 Minuten2 entspricht einer Standardabweichung von 3 Minuten.
VarKoeff
Der Variationskoeffizient (als KOV bezeichnet) ist ein Maß der Streubreite, das die Streuung der Daten relativ zum Mittelwert beschreibt. Der Variationskoeffizient ist korrigiert, so dass die Werte auf eine dimensionslosen Skala liegen. Aufgrund dieser Korrektur können Sie den Variationskoeffizienten anstelle der Standardabweichung verwenden, um die Streuung in Daten zu vergleichen, die unterschiedliche Einheiten oder stark voneinander abweichende Mittelwerte aufweisen.
Interpretation
Je größer der Variationskoeffizient, desto größer ist die Streubreite der Daten.
| Großer Behälter | Kleiner Behälter |
|---|---|
| Variationskoeffizient = 100 * 0,4 Cups / 16 Cups = 2,5 | Variationskoeffizient = 100 * 0,08 Cups / 1 Cup = 8 |
Q1
Quartile sind die drei Werte – das erste Quartil bei 25 % (Q1), das zweite Quartil bei 50 % (Q2 oder Median) und das dritte Quartil bei 75 % (Q3) –, die eine Stichprobe von geordneten Daten in vier gleiche Teile teilen.
Das erste Quartil ist das 25. Perzentil und gibt an, dass 25 % der Daten kleiner als oder gleich diesem Wert sind.
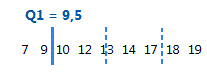
Für diese geordneten Daten beträgt das erste Quartil (Q1) 9,5. Das heißt, 25 % der Daten sind kleiner oder gleich 9,5.
Median
Der Median ist der Mittelpunkt des Datensatzes. Dieser Wert gibt den Punkt an, an dem die Hälfte der Beobachtungen über dem Wert und die Hälfte der Beobachtungen unter dem Wert liegen. Der Median wird durch Bilden einer Rangfolge der Beobachtungen und Ermitteln der Beobachtung an der Stelle [N + 1] / 2 in der Rangfolge bestimmt. Wenn die Daten eine gerade Anzahl von Beobachtungen enthalten, ist der Median der Durchschnittswert der Beobachtungen an den Stellen N / 2 und [N / 2] + 1 in der Rangfolge.

Für diese geordneten Daten ist der Median 13. Das heißt, die Hälfte der Werte sind kleiner oder gleich 13, und die andere Hälfte der Werte sind größer oder gleich 13. Wenn Sie eine weitere Beobachtung mit dem Wert 20 hinzufügen, beträgt der Median 13,5; dies ist der Durchschnitt zwischen der 5. Beobachtung (13) und der 6. Beobachtung (14).
Interpretation

Symmetrisch

Nicht symmetrisch
Bei der symmetrischen Verteilung ähneln sich der Mittelwert (blaue Linie) und der Median (orangefarbene Linie) so sehr, dass die Linien nicht ohne weiteres unterschieden werden können. Die nicht symmetrische Verteilung ist jedoch rechtsschief.
Q3
Quartile sind die drei Werte – das erste Quartil bei 25 % (Q1), das zweite Quartil bei 50 % (Q2 oder Median) und das dritte Quartil bei 75 % (Q3) –, die eine Stichprobe von geordneten Daten in vier gleiche Teile teilen.
Das dritte Quartil ist das 75. Perzentil und gibt an, dass 75 % der Daten kleiner als oder gleich diesem Wert sind.
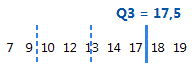
Für diese geordneten Daten beträgt das dritte Quartil (Q3) 17,5. Das heißt, 75 % der Daten sind kleiner oder gleich 17,5.
IQR
Der Interquartilbereich (IQR) ist der Abstand zwischen dem ersten Quartil (Q1) und dem dritten Quartil (Q3). 50 % der Daten liegen in diesem Bereich.

Für diese geordneten Daten beträgt der Interquartilbereich 8 (17,5 – 9,5 = 8). Das heißt, die mittleren 50 % der Daten liegen zwischen 9,5 und 17,5.
Interpretation
Verwenden Sie den Interquartilbereich, um die Streubreite der Daten zu beschreiben. Mit zunehmender Streubreite der Daten erhöht sich auch der IQR.
TrMW
Der Mittelwert der Daten ohne die höchsten 5 % und die niedrigsten 5 % der Werte.
Mit dem getrimmten Mittel können Sie unterbinden, dass sich sehr große oder sehr kleine Werte auf den Mittelwert auswirken. Wenn die Daten Ausreißer enthalten, ist das getrimmte Mittel möglicherweise eine besser geeignetes Maß der Zentraltendenz als der Mittelwert.
Summe
Die Summe stellt die Gesamtsumme aller Datenwerte dar. Außerdem wird die Summe bei bestimmten statistischen Berechnungen verwendet, zum Beispiel für den Mittelwert und die Standardabweichung.
Minimum
Das Minimum ist der kleinste Datenwert.
In diesen Daten ist das Minimum 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretation
Verwenden Sie das Minimum, um einen möglichen Ausreißer oder einen Fehler bei der Dateneingabe zu identifizieren. Eine der einfachsten Möglichkeiten, um die Streubreite in den Daten zu ermitteln, ist ein Vergleich von Minimum und Maximum. Wenn der Wert des Minimums sehr niedrig ist, selbst bei Berücksichtigung des Zentrums, der Streubreite und der Form der Daten, untersuchen Sie die Ursache für den Extremwert.
Maximum
Das Maximum ist der größte Datenwert.
In diesen Daten ist das Maximum 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretation
Verwenden Sie das Maximum, um einen möglichen Ausreißer oder einen Fehler bei der Dateneingabe zu identifizieren. Eine der einfachsten Möglichkeiten, um die Streubreite in den Daten zu ermitteln, ist ein Vergleich von Minimum und Maximum. Wenn der Wert des Maximums sehr hoch ist, selbst bei Berücksichtigung des Zentrums, der Streubreite und der Form der Daten, untersuchen Sie die Ursache für den Extremwert.
Spannweite
Die Spannweite ist die Differenz zwischen dem größten und dem kleinsten Datenwert in der Stichprobe. Die Spannweite stellt das Intervall dar, das alle Datenwerte enthält.
Interpretation
Verwenden Sie die Spannweite, um das Ausmaß der Streuung in den Daten zu untersuchen. Eine große Spannweite gibt eine größere Streuung in den Daten an. Eine kleine Spannweite gibt an, dass die Streuung in den Daten geringer ist. Da die Spannweite mit nur zwei Datenwerten berechnet wird, ist sie bei kleinen Datensätzen am nützlichsten.
SSQ
Die unkorrigierte Summe der Quadrate ist die Summe der Quadrate jedes Werts in der Spalte. Wenn die Spalte beispielsweise x1, x2, ... , xn enthält, entspricht die Summe der Quadrate (x12 + x22 + ... + xn2). Anders als die korrigierte Summe der Quadrate umfasst die unkorrigierte Summe der Quadrate Fehler. Die Datenwerte werden quadriert, ohne vorher den Mittelwert zu subtrahieren.
Schiefe
Die Schiefe gibt das Ausmaß an, in dem die Daten asymmetrisch sind.
Interpretation
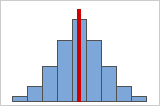
Abbildung A
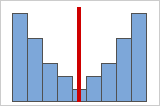
Abbildung B
Symmetrische oder nicht schiefe Verteilungen
Mit zunehmender Symmetrie der Daten nähert sich deren Schiefewert null an. Abbildung A zeigt normalverteilte Daten, die per definitionem eine relativ geringe Schiefe aufweisen. Wenn Sie eine Linie durch die Mitte dieses Histogramms von normalverteilten Daten zeichnen, wird ersichtlich, dass die beiden Seiten einander spiegeln. Eine fehlende Schiefe allein impliziert jedoch keine Normalverteilung. Abbildung B zeigt eine Verteilung, bei der beide Seiten einander immer noch spiegeln, die Daten jedoch keineswegs normalverteilt sind.
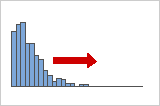
Positiv schiefe oder rechtsschiefe Verteilungen
Positiv schiefe oder rechtsschief verteilte Daten werden so bezeichnet, weil der Randbereich der Verteilung nach rechts zeigt und der Schiefewert größer als 0 (d. h. positiv) ist. Gehaltsdaten weisen häufig eine solche Schiefe auf: Viele Mitarbeiter eines Unternehmens erhalten ein relativ kleines Gehalt, während zunehmend weniger Personen sehr hohe Gehälter beziehen.
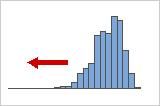
Negativ schiefe oder linksschiefe Verteilungen
Linksschiefe oder negativ schiefe Daten werden so bezeichnet, weil der Randbereich der Verteilung nach links weist und ein negativer Schiefewert vorliegt. Daten zu Ausfallraten sind häufig linksschief. Ein Beispiel sind Glühlampen: Sehr wenige brennen sofort durch, und die überwiegende Mehrzahl weist eine lange Lebensdauer auf.
Kurtosis
Die Kurtosis gibt an, wie weit die Randbereiche einer Verteilung von der Normalverteilung abweichen.
Interpretation
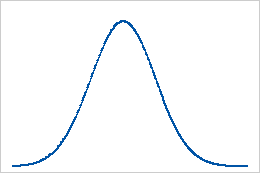
Basislinie: Kurtosis-Wert 0
Normalverteilte Daten bilden die Basislinie für die Kurtosis. Der Kurtosis-Wert 0 gibt an, dass die Daten der Normalverteilung perfekt folgen. Wenn ein Kurtosis-Wert wesentlich von 0 abweicht, kann dies darauf hinweisen, dass die Daten nicht normalverteilt sind.

Positive Kurtosis
Ein positiver Kurtosis-Wert für eine Verteilung deutet darauf hin, dass sich die Verteilung durch stärker ausgeprägte Randbereiche als die Normalverteilung auszeichnet. Daten, die einer t-Verteilung folgen, weisen beispielsweise einen positiven Kurtosis-Wert auf. Die durchgezogene Linie stellt die Normalverteilung und die gepunktete Linie eine Verteilung mit einem positiven Kurtosis-Wert dar.
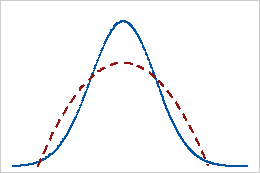
Negative Kurtosis
Ein negativer Kurtosis-Wert für eine Verteilung deutet darauf hin, dass sich die Verteilung durch schwächer ausgeprägte Randbereiche als die Normalverteilung auszeichnet. Daten, die einer Betaverteilung folgen, deren erster und zweiter Formparameter gleich 2 ist, weisen beispielsweise einen negativen Kurtosis-Wert auf. Die durchgezogene Linie stellt die Normalverteilung und die gepunktete Linie eine Verteilung mit einem negativen Kurtosis-Wert dar.
MSSD
MSSD ist das Mittel der quadrierten sukzessiven Differenzen. MSSD ist eine Schätzung der Varianz. Eine mögliche Anwendung des MSSD ist der Test, ob eine Folge von Beobachtungen zufällig ist. In der Qualitätskontrolle ist eine mögliche Anwendung des MSSD die Schätzung der Streuung bei einer Teilgruppengröße = 1.
N
Die Anzahl der nicht fehlenden Werte in der Stichprobe.
| Gesamtanzahl | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N fehlend
Die Anzahl der fehlenden Werte in der Stichprobe. Die Anzahl der fehlenden Werte bezieht sich auf Zellen, die das Symbol für fehlende Werte * enthalten.
| Gesamtanzahl | N | N fehlend |
|---|---|---|
| 149 | 141 | 8 |
Anzahl
Die Gesamtanzahl der Beobachtungen in der Spalte. Hiermit wird die Summe von N fehlend und N nicht fehlend dargestellt.
| Anzahl | N | N fehlend |
|---|---|---|
| 149 | 141 | 8 |
KumN
| Klassenstufe | Anzahl | KumN | Berechnung |
|---|---|---|---|
| 1 | 49 | 49 | 49 |
| 2 | 58 | 107 | 49 + 58 |
| 3 | 52 | 159 | 49 + 58 + 52 |
| 4 | 60 | 219 | 49 + 58 + 52 + 60 |
| 5 | 48 | 267 | 49 + 58 + 52 + 60 + 48 |
| 6 | 55 | 322 | 49 + 58 + 52 + 60 + 48 + 55 |
Prozent
Der Prozentsatz der Beobachtungen in jeder Gruppe der Gruppierungsvariablen. Im folgenden Beispiel liegen vier Gruppen vor: Linie 1, Linie 2, Linie 3 und Linie 4.
| Gruppe (Gruppierungsvariable) | Prozent |
|---|---|
| Linie 1 | 16 |
| Linie 2 | 20 |
| Linie 3 | 36 |
| Linie 4 | 28 |
KumP
Der kumulierte Prozentsatz ist die kumulierte Summe der Prozentsätze für jede Gruppe der Gruppierungsvariablen. Im folgenden Beispiel weist die Gruppierungsvariable vier Gruppen auf: Linie 1, Linie 2, Linie 3 und Linie 4.
| Gruppe (Gruppierungsvariable) | Prozent | KumP |
|---|---|---|
| Linie 1 | 16 | 16 |
| Linie 2 | 20 | 36 |
| Linie 3 | 36 | 72 |
| Linie 4 | 28 | 100 |
