In diesem Thema
Schritt 1: Bestimmen eines Konfidenzintervalls für die Mittelwertdifferenz der Grundgesamtheit
Betrachten Sie zuerst die Mittelwertdifferenz, und untersuchen Sie anschließend das Konfidenzintervall. Die Mittelwertdifferenz ist der Durchschnitt der Differenzen zwischen den verbundenen Beobachtungen in der Stichprobe.
Die Mittelwertdifferenz ist ein Schätzwert der Mittelwertdifferenz der Grundgesamtheit. Da die Mittelwertdifferenz auf Stichprobendaten und nicht auf der vollständigen Grundgesamtheit basiert, ist es unwahrscheinlich, dass die Mittelwertdifferenz der Stichprobe gleich der Mittelwertdifferenz der Grundgesamtheit ist. Verwenden Sie das Konfidenzintervall der Differenz, um die Mittelwertdifferenz der Grundgesamtheit besser schätzen zu können.
Das Konfidenzintervall ist ein Bereich wahrscheinlicher Werte für die Differenz der Mittelwerte der Grundgesamtheiten der verbundenen Beobachtungen. Ein 95%-Konfidenzniveau gibt beispielsweise an, dass bei einer Entnahme von 100 Zufallsstichproben aus der Grundgesamtheit die Konfidenzintervalle für voraussichtlich ca. 95 der Stichproben die Mittelwertdifferenz der Grundgesamtheit enthalten. Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihrer Ergebnisse beurteilen. Bestimmen Sie anhand Ihrer Fachkenntnisse, ob das Konfidenzintervall Werte umfasst, die in der jeweiligen Situation von praktischer Signifikanz sind. Wenn das Intervall zu breit und damit nicht hilfreich ist, erwägen Sie, den Stichprobenumfang zu vergrößern. Weitere Informationen finden Sie unter Möglichkeiten zum Erhöhen der Genauigkeit des Konfidenzintervalls.
Schätzwert für gepaarte Differenz
| Mittelwert | StdAbw | SE des Mittelwerts | 95%-KI für µ_Differenz |
|---|---|---|---|
| 2,200 | 3,254 | 0,728 | (0,677; 3,723) |
Wichtigste Ergebnisse: Mittelwert, 95%-KI für Mittelwertdifferenz
In diesen Ergebnissen beträgt der Schätzwert der Mittelwertdifferenz der Grundgesamtheit für den Ruhepuls 2,2. Sie können sich zu 95 % sicher sein, dass die Mittelwertdifferenz der Grundgesamtheit zwischen 0,677 und 3,723 liegt.
Schritt 2: Bestimmen, ob die Testergebnisse statistisch signifikant sind
- p-Wert ≤ α: Die Differenz zwischen den Mittelwerten ist statistisch signifikant (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück. Sie können schlussfolgern, dass die Differenz zwischen den Mittelwerten der Grundgesamtheiten ungleich der hypothetischen Differenz ist. Wenn Sie keine hypothetische Differenz angegeben haben, testet Minitab, ob zwischen den Mittelwerten keine Differenz vorliegt (Hypothesendifferenz = 0). Bestimmen Sie anhand Ihres Fachwissens, ob die Differenz praktisch signifikant ist. Weitere Informationen finden Sie unter Statistische und praktische Signifikanz.
- p-Wert > α: Die Differenz zwischen den Mittelwerten ist statistisch nicht signifikant (H0 nicht verwerfen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen nicht genügend Anzeichen für die Schlussfolgerung vor, dass die Differenz zwischen den Mittelwerten der verbundenen Beobachtungen statistisch signifikant ist. Vergewissern Sie sich, dass der Test über eine ausreichende Trennschärfe verfügt, um eine praktisch signifikante Differenz zu erkennen. Weitere Informationen finden Sie unter Trennschärfe und Stichprobenumfang für t-Test, verbundene Stichproben.
Test
| Nullhypothese | H₀: μ_Differenz = 0 |
|---|---|
| Alternativhypothese | H₁: μ_Differenz ≠ 0 |
| t-Wert | p-Wert |
|---|---|
| 3,02 | 0,007 |
Wichtigstes Ergebnis: p-Wert
In diesen Ergebnissen besagt die Nullhypothese, dass die Mittelwertdifferenz für den Ruhepuls der Patienten vor und nach einem Laufprogramm 0 ist. Da der p-Wert 0,007 beträgt und somit niedriger als das Signifikanzniveau 0,05 ist, weisen Sie die Nullhypothese zurück und folgern, dass es eine Differenz beim Ruhepuls der Patienten vor und nach dem Laufprogramm gibt.
Schritt 3: Prüfen der Daten auf Probleme
Probleme mit Ihren Daten, z. B. Schiefe und Ausreißer, können die Ergebnisse beeinträchtigen. Suchen Sie anhand von Grafiken nach Schiefe, und ermitteln Sie potenzielle Ausreißer.
Untersuchen Sie die Streubreite der Daten, um zu ermitteln, ob die Daten schief sind.
Wenn die Daten schief sind, liegen die meisten Datenwerte am oberen oder unteren Rand der Grafik. Häufig lässt sich die Schiefe am einfachsten mit einem Histogramm oder einem Boxplot erkennen.
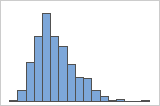
Rechtsschief
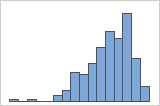
Linksschief
Das Histogramm mit rechtsschiefen Daten zeigt Wartezeiten. Die meisten Wartezeiten sind relativ kurz, und nur wenige Wartezeiten sind lang. Das Histogramm mit linksschiefen Daten zeigt Ausfallzeiten. Nur wenige Elemente fallen sofort aus, während viel mehr Elemente zu späteren Zeitpunkten ausfallen.
Stark schiefe Daten können die Gültigkeit des p-Werts beeinträchtigen, wenn die Stichprobe klein ist (weniger als 20 Werte). Wenn die Daten stark schief sind und eine kleine Stichprobe vorliegt, erwägen Sie, den Stichprobenumfang zu vergrößern.
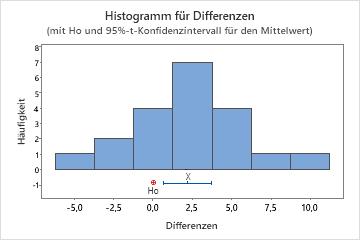
In diesem Histogramm scheinen die Daten keine starke Schiefe aufzuweisen.
Identifizieren von Ausreißern
Ausreißer, d. h. Datenwerte, die weit entfernt von anderen Datenwerten liegen, können sich stark auf die Ergebnisse der Analyse auswirken. Häufig können Ausreißer am einfachsten in einem Boxplot identifiziert werden.
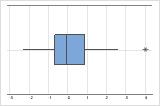
In einem Boxplot werden Ausreißer mit einem Sternchen (*) gekennzeichnet.
Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (so genannte Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse. Weitere Informationen finden Sie unter Identifizieren von Ausreißern.
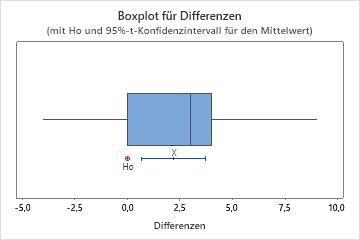
In diesem Boxplot gibt es keine Ausreißer.
