In diesem Thema
N
Der Stichprobenumfang (N) gibt die Gesamtzahl der Beobachtungen in der Stichprobe an.
Interpretation
Der Stichprobenumfang wirkt sich auf das Konfidenzintervall und auf die Trennschärfe des Tests aus.
Eine größere Stichprobe führt in der Regel zu einem schmaleren Konfidenzintervall. Bei größeren Stichprobenumfängen verfügt der Test außerdem über eine höhere Trennschärfe zum Erkennen einer Differenz. Weitere Informationen finden Sie unter Was ist die Trennschärfe?.
Mittelwert
Minitab zeigt den Mittelwert für jede Stichprobe und den Mittelwert der Differenzen zwischen den verbundenen Beobachtungen an.
Der Mittelwert fasst die Stichprobenwerte in einem einzigen Wert zusammen, der das Zentrum der Daten darstellt. Der Mittelwert ist der Durchschnitt der Daten; hierbei handelt es sich um die Summe aller Beobachtungen dividiert durch die Anzahl der Beobachtungen.
Interpretation
Die Mittelwertdifferenz ist ein Schätzwert der Mittelwertdifferenz der Grundgesamtheit.
Da die Mittelwertdifferenz auf Stichprobendaten und nicht auf der vollständigen Grundgesamtheit basiert, ist es unwahrscheinlich, dass die Mittelwertdifferenz der Stichprobe gleich der Mittelwertdifferenz der Grundgesamtheit ist. Verwenden Sie das Konfidenzintervall der Differenz, um die Mittelwertdifferenz der Grundgesamtheit besser schätzen zu können.
StdAbw
Die Standardabweichung ist das am häufigsten verwendete Maß für die Streuung bzw. die Streubreite der Daten um den Mittelwert. Die Standardabweichung einer Grundgesamtheit wird häufig mit dem Zeichen σ (Sigma) angegeben, während mit s die Standardabweichung einer Stichprobe dargestellt wird. Eine zufällige oder natürliche Streuung eines Prozesses wird häufig auch als Rauschen bezeichnet.
Für die Standardabweichung wird die gleiche Einheit wie für die Daten verwendet.
Interpretation
Verwenden Sie die Standardabweichung, um die Streubreite der Daten um den Mittelwert zu ermitteln. Ein höherer Wert der Standardabweichung verweist auf eine größere Streubreite der Daten. Eine Faustregel für die Normalverteilung besagt, dass etwa 68 % der Werte innerhalb einer Standardabweichung vom Mittelwert, 95 % der Werte innerhalb zwei Standardabweichungen und 99,7 % der Werte innerhalb drei Standardabweichungen liegen.
Die Standardabweichung der Stichprobendaten ist ein Schätzwert der Standardabweichung der Grundgesamtheit. Die Standardabweichung wird verwendet, um das Konfidenzintervall und den p-Wert zu berechnen. Ein größerer Wert produziert weniger präzise (breitere) Konfidenzintervalle und Tests mit geringerer Trennschärfe.

Krankenhaus 1
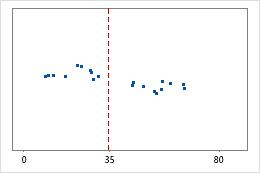
Krankenhaus 2
Zeit bis zur Entlassung in Krankenhäusern
Verwaltungsangestellte zeichnen die Zeit bis zur Entlassung von Patienten auf, die in der Notaufnahme zweier Krankenhäuser behandelt werden. Obwohl die durchschnittliche Zeit bis zur Entlassung in etwa identisch ist (35 Minuten), weichen die Standardabweichungen signifikant voneinander ab. Die Standardabweichung für Krankenhaus 1 beträgt etwa 6. Im Durchschnitt weicht die Zeit bis zur Entlassung eines Patienten um etwa 6 Minuten vom Mittelwert (gestrichelte Linie) ab. Die Standardabweichung für Krankenhaus 2 beträgt etwa 20. Im Durchschnitt weicht die Zeit bis zur Entlassung eines Patienten um ca. 20 Minuten vom Mittelwert (gestrichelte Linie) ab.
SE des Mittelwerts
Der Standardfehler des Mittelwerts (SE des Mittelwerts) schätzt die Streuung zwischen den Stichprobenmittelwerten, die Sie erhalten würden, wenn Sie wiederholt Stichproben aus derselben Grundgesamtheit ziehen. Mit dem Standardfehler des Mittelwerts wird die Streuung zwischen Stichproben geschätzt, während mit der Standardabweichung die Streuung innerhalb einer Stichprobe gemessen wird.
Angenommen bei einer Zufallsstichprobe von 312 Lieferungen beträgt die mittlere Lieferzeit 3,80 Tage, mit einer Standardabweichung von 1,43 Tagen. Diese Werte ergeben einen Standardfehler des Mittelwerts von 0,08 Tagen (1,43 dividiert durch die Quadratwurzel von 312). Würden Sie mehrere zufällig ausgewählte Stichproben gleicher Größe aus derselben Grundgesamtheit ziehen, betrüge die Standardabweichung der verschiedenen Stichprobenmittelwerte etwa 0,08 Tage.
Interpretation
Verwenden Sie den Standardfehler des Mittelwerts, um zu bestimmen, wie präzise der Mittelwert der Stichprobe den Mittelwert der Grundgesamtheit schätzt.
Ein kleinerer Wert des Standardfehlers des Mittelwerts zeigt einen präziseren Schätzwert für den Mittelwert der Grundgesamtheit an. Im Allgemeinen ergibt eine größere Standardabweichung einen größeren Standardfehler des Mittelwerts und einen weniger präzisen Schätzwert für den Mittelwert der Grundgesamtheit. Ein größerer Stichprobenumfang ergibt einen kleineren Standardfehler des Mittelwerts und einen präziseren Schätzwert für den Mittelwert der Grundgesamtheit.
In Minitab wird mit dem Standardfehler des Mittelwerts das Konfidenzintervall berechnet.
Konfidenzintervall (KI) und Konfidenzgrenzen
Das Konfidenzintervall ist ein Bereich wahrscheinlicher Werte für die Mittelwertdifferenz der Grundgesamtheit. Da die Stichproben zufällig sind, ist es unwahrscheinlich, dass zwei Stichproben aus einer Grundgesamtheit identische Konfidenzintervalle ergeben. Wenn Sie die Stichprobennahme jedoch viele Male wiederholen, enthält ein bestimmter Prozentsatz der resultierenden Konfidenzintervalle oder -grenzen die unbekannte Mittelwertdifferenz der Grundgesamtheit. Der Prozentsatz dieser Konfidenzintervalle oder -grenzen, die die Mittelwertdifferenz enthalten, stellt das Konfidenzniveau des Intervalls dar. Ein 95%-Konfidenzniveau gibt beispielsweise an, dass bei einer Entnahme von 100 Zufallsstichproben aus der Grundgesamtheit die Konfidenzintervalle für voraussichtlich ca. 95 der Stichproben die Mittelwertdifferenz der Grundgesamtheit enthalten.
Eine Obergrenze ist der Wert, der wahrscheinlich größer als die Mittelwertdifferenz der Grundgesamtheit ist. Eine Untergrenze ist der Wert, der wahrscheinlich kleiner als die Mittelwertdifferenz der Grundgesamtheit ist.
Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihrer Ergebnisse beurteilen. Bestimmen Sie anhand Ihrer Fachkenntnisse, ob das Konfidenzintervall Werte umfasst, die in der jeweiligen Situation von praktischer Signifikanz sind. Wenn das Intervall zu breit und damit nicht hilfreich ist, erwägen Sie, den Stichprobenumfang zu vergrößern. Weitere Informationen finden Sie unter Möglichkeiten zum Erhöhen der Genauigkeit des Konfidenzintervalls.
Schätzwert für gepaarte Differenz
| Mittelwert | StdAbw | SE des Mittelwerts | 95%-KI für µ_Differenz |
|---|---|---|---|
| 2,200 | 3,254 | 0,728 | (0,677; 3,723) |
In diesen Ergebnissen beträgt der Schätzwert der Mittelwertdifferenz der Grundgesamtheit für den Ruhepuls 2,2. Sie können sich zu 95 % sicher sein, dass die Mittelwertdifferenz der Grundgesamtheit zwischen 0,677 und 3,723 liegt.
Nullhypothese und Alternativhypothese
- Nullhypothese
- Die Nullhypothese besagt, dass ein Parameter einer Grundgesamtheit (z. B. der Mittelwert, die Standardabweichung usw.) gleich einem Hypothesenwert ist. Die Nullhypothese ist oft eine anfängliche Behauptung auf der Grundlage von früheren Analysen oder Fachwissen.
- Alternativhypothese
- Die Alternativhypothese besagt, dass ein Parameter einer Grundgesamtheit kleiner, größer oder ungleich dem hypothetischen Wert in der Nullhypothese ist. Die Alternativhypothese ist die Hypothese, die Sie als wahr annehmen oder deren Wahrheit Sie nachweisen möchten.
In der Ausgabe können Sie mit Hilfe der Nullhypothese und der Alternativhypothese überprüfen, ob Sie den korrekten Wert für die Testdifferenz eingegeben haben.
t-Wert
Der t-Wert ist der beobachtete Wert der Teststatistik für t-Tests, mit der die Differenz zwischen einer beobachteten Stichprobenstatistik und deren hypothetischem Parameter der Grundgesamtheit in Einheiten des Standardfehlers gemessen wird.
Interpretation
Sie können den t-Wert mit den kritischen Werten der t-Verteilung vergleichen, um zu bestimmen, ob die Nullhypothese zurückzuweisen ist. Es jedoch im Allgemeinen praktischer, hierfür den p-Wert des Tests heranzuziehen.
Um zu bestimmen, ob die Nullhypothese zurückzuweisen ist, vergleichen Sie den t-Wert mit dem kritischen Wert. Der kritische Wert ist tα/2, n-1 für einen beidseitigen Test und tα, n-1 für einen einseitigen Test. Wenn bei einem beidseitigen Test der Absolutwert des t-Werts größer als der kritische Wert ist, weisen Sie die Nullhypothese zurück. Andernfalls verwerfen Sie die Nullhypothese nicht. Sie können den kritischen Wert in Minitab berechnen oder diesen einer in den meisten Fachbüchern vorhandenen Tabelle für die t-Verteilung entnehmen. Weitere Informationen finden Sie unter Verwenden der inversen kumulativen Verteilungsfunktion (ICDF); klicken Sie dort auf „Verwenden der ICDF zum Berechnen von kritischen Werten“.
p-Wert
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Ein kleinerer p-Wert liefert stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Interpretation
Verwenden Sie den p-Wert, um zu ermitteln, ob der Mittelwert der Differenzen der Grundgesamtheiten statistisch vom hypothetischen Mittelwert der Differenzen abweicht.
- p-Wert ≤ α: Die Differenz zwischen den Mittelwerten ist statistisch signifikant (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück. Sie können schlussfolgern, dass die Differenz zwischen den Mittelwerten der Grundgesamtheiten ungleich der hypothetischen Differenz ist. Wenn Sie keine hypothetische Differenz angegeben haben, testet Minitab, ob zwischen den Mittelwerten keine Differenz vorliegt (Hypothesendifferenz = 0). Bestimmen Sie anhand Ihres Fachwissens, ob die Differenz praktisch signifikant ist. Weitere Informationen finden Sie unter Statistische und praktische Signifikanz.
- p-Wert > α: Die Differenz zwischen den Mittelwerten ist statistisch nicht signifikant (H0 nicht verwerfen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen nicht genügend Anzeichen für die Schlussfolgerung vor, dass die Differenz zwischen den Mittelwerten der verbundenen Beobachtungen statistisch signifikant ist. Vergewissern Sie sich, dass der Test über eine ausreichende Trennschärfe verfügt, um eine praktisch signifikante Differenz zu erkennen. Weitere Informationen finden Sie unter Trennschärfe und Stichprobenumfang für t-Test, verbundene Stichproben.
Histogramm
In einem Histogramm werden die Stichprobenwerte in eine Reihe von Intervallen unterteilt, und die Häufigkeiten der Datenwerte in jedem Intervall werden in Form eines Balkens abgebildet.
Interpretation
Verwenden Sie ein Histogramm, um die Form und Streubreite der Daten auszuwerten. Für Histogramme sollte der Stichprobenumfang größer als 20 sein.
- Schiefe Daten
-
Untersuchen Sie die Streubreite der Daten, um zu ermitteln, ob die Daten schief sind. Wenn Daten schief sind, befinden sich die meisten Daten im oberen oder unteren Teil der Grafik. Schiefe ist häufig am einfachsten mit einem Histogramm oder Boxplot zu erkennen.
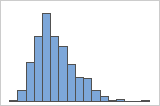
Rechtsschief
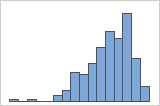
Linksschief
Das Histogramm mit rechtsschiefen Daten zeigt Wartezeiten. Der Großteil der Wartezeiten ist relativ kurz, nur wenige Wartezeiten sind lang. Das Histogramm mit linksschiefen Daten zeigt Daten zu Ausfallzeiten. Einige Elemente fallen sofort aus, deutlich mehr Elemente fallen später aus.
Daten, die eine sehr starke Schiefe aufweisen, können die Gültigkeit des p-Werts beeinträchtigen, wenn die Stichprobe klein ist (weniger als 20 Werte). Wenn Ihre Daten stark schief sind und Ihre Stichprobe klein ist, ziehen Sie in Betracht, die Stichprobe zu vergrößern.
- Ausreißer
-
Ausreißer, d. h. Daten, die sich weit entfernt von den anderen Datenwerten befinden, können starke Auswirkungen auf die Ergebnisse Ihrer Analyse haben. Häufig lassen sich Ausreißer am einfachsten in einem Boxplot erkennen.

In einem Histogramm stellen einzelne Balken an den Enden mögliche Ausreißer dar.
Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (so genannte Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse. Weitere Informationen finden Sie unter Identifizieren von Ausreißern.
Einzelwertdiagramm
Ein Einzelwertdiagramm veranschaulicht die einzelnen Werte in der Stichprobe. Jeder Kreis stellt eine Beobachtung dar. Ein Einzelwertdiagramm ist besonders dann nützlich, wenn Ihnen relativ wenige Beobachtungen vorliegen und Sie außerdem den Effekt jeder Beobachtung auswerten müssen.
Interpretation
Verwenden Sie ein Einzelwertdiagramm, um die Streubreite der Daten zu untersuchen und potenzielle Ausreißer zu identifizieren. Für Einzelwertdiagramme sollte der Stichprobenumfang größer als 50 sein.
- Schiefe Daten
-
Untersuchen Sie die Streubreite der Daten, um zu ermitteln, ob die Daten schief sind. Wenn Daten schief sind, befinden sich die meisten Daten im oberen oder unteren Teil der Grafik. Schiefe ist häufig am einfachsten mit einem Histogramm oder Boxplot zu erkennen.
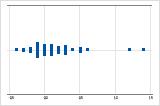
Rechtsschief

Linksschief
Das Einzelwertdiagramm mit rechtsschiefen Daten zeigt Wartezeiten. Der Großteil der Wartezeiten ist relativ kurz, nur wenige Wartezeiten sind lang. Das Einzelwertdiagramm mit linksschiefen Daten zeigt Daten zu Ausfallzeiten. Einige Elemente fallen sofort aus, deutlich mehr Elemente fallen später aus.
Daten, die eine sehr starke Schiefe aufweisen, können die Gültigkeit des p-Werts beeinträchtigen, wenn die Stichprobe klein ist (weniger als 20 Werte). Wenn Ihre Daten stark schief sind und Ihre Stichprobe klein ist, ziehen Sie in Betracht, die Stichprobe zu vergrößern.
- Ausreißer
-
Ausreißer, d. h. Daten, die sich weit entfernt von den anderen Datenwerten befinden, können starke Auswirkungen auf die Ergebnisse Ihrer Analyse haben. Häufig lassen sich Ausreißer am einfachsten in einem Boxplot erkennen.
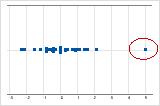
In einem Einzelwertdiagramm weisen ungewöhnlich hohe oder niedrige Datenwerte auf mögliche Ausreißer hin.
Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (so genannte Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse. Weitere Informationen finden Sie unter Identifizieren von Ausreißern.
Boxplot
Ein Boxplot stellt eine grafische Zusammenfassung der Verteilung einer Stichprobe dar. Das Boxplot zeigt die Form, Zentraltendenz und Streuung der Daten.
Interpretation
Verwenden Sie ein Boxplot, um die Streubreite der Daten zu untersuchen und potenzielle Ausreißer zu identifizieren. Für Boxplots sollte der Stichprobenumfang größer als 20 sein.
- Schiefe Daten
-
Untersuchen Sie die Streubreite der Daten, um zu ermitteln, ob die Daten schief sind. Wenn Daten schief sind, befinden sich die meisten Daten im oberen oder unteren Teil der Grafik. Schiefe ist häufig am einfachsten mit einem Histogramm oder Boxplot zu erkennen.
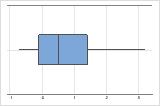
Rechtsschief
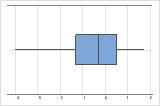
Linksschief
Das Boxplot mit rechtsschiefen Daten zeigt Wartezeiten. Der Großteil der Wartezeiten ist relativ kurz, nur wenige Wartezeiten sind lang. Das Boxplot mit linksschiefen Daten zeigt Daten zu Ausfallzeiten. Einige Elemente fallen sofort aus, deutlich mehr Elemente fallen später aus.
Daten, die eine sehr starke Schiefe aufweisen, können die Gültigkeit des p-Werts beeinträchtigen, wenn die Stichprobe klein ist (weniger als 20 Werte). Wenn Ihre Daten stark schief sind und Ihre Stichprobe klein ist, ziehen Sie in Betracht, die Stichprobe zu vergrößern.
- Ausreißer
-
Ausreißer, d. h. Daten, die sich weit entfernt von den anderen Datenwerten befinden, können starke Auswirkungen auf die Ergebnisse Ihrer Analyse haben. Häufig lassen sich Ausreißer am einfachsten in einem Boxplot erkennen.
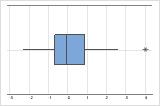
In einem Boxplot werden Ausreißer mit einem Asterisk (*) gekennzeichnet.
Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (so genannte Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse. Weitere Informationen finden Sie unter Identifizieren von Ausreißern.
