Interpretieren der wichtigsten Ergebnisse für Test auf Ausreißer

Führen Sie die folgenden Schritte aus, um einen Test auf Ausreißer zu interpretieren. Zu den wichtigsten Ausgaben zählen der p-Wert, der Ausreißer und das Diagramm der Ausreißer.

In diesem Thema

Schritt 1: Bestimmen, ob ein Ausreißer vorhanden ist
Schritt 2: Wert des Ausreißers ermitteln
Schritt 3: Ausreißer visuell identifizieren

Schritt 1: Bestimmen, ob ein Ausreißer vorhanden ist

Um zu ermitteln, ob ein Ausreißer vorhanden ist, vergleichen Sie den p-Wert mit dem Signifikanzniveau. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko der Schlussfolgerung, dass auf einen vorhandenen Ausreißer geschlossen wird, während tatsächlich kein Ausreißer vorhanden ist, von 5 %.

p-Wert ≤ α: Es ist ein Ausreißer vorhanden (H₀ verwerfen): Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass ein Ausreißer vorhanden ist. Versuchen Sie, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind.
p-Wert > α: Es kann nicht gefolgert werden, dass ein Ausreißer vorhanden ist (H₀ nicht verwerfen): Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück, da keine ausreichenden Hinweise für die Schlussfolgerung vorliegen, dass ein Ausreißer vorhanden ist. Vergewissern Sie sich, dass der Test über eine ausreichende Trennschärfe verfügt, um einen Ausreißer zu erkennen. Weitere Informationen finden Sie unter Erhöhen der Trennschärfe.

Methode

Nullhypothese	Alle Datenwerte stammen aus derselben normalverteilten Grundgesamtheit.
Alternativhypothese	Kleinster Datenwert ist ein Ausreißer
Signifikanzniveau	α = 0,05

Grubbs-Test

Variable	N	Mittelwert	StdAbw	Min	Max	G	p
Bruchfestigkeit	14	123,4	46,3	12,4	193,1	2,40	0,044

Ausreißer

Variable	Zeile	Ausreißer
Bruchfestigkeit	10	12,38

Wichtigstes Ergebnis: p-Wert

In diesen Ergebnissen besagt die Nullhypothese, dass alle Datenwerte aus derselben normalverteilten Grundgesamtheit stammen. Da der p-Wert 0,044 beträgt und somit niedriger als das Signifikanzniveau von 0,05 ist, wird entschieden, die Nullhypothese zu verwerfen und zu folgern, dass ein Ausreißer vorhanden ist.

Schritt 2: Wert des Ausreißers ermitteln

Wenn im Test ein Ausreißer in den Daten identifiziert wird, zeigt Minitab eine Ausreißertabelle an. Bestimmen Sie anhand der Ausreißertabelle den Wert des Ausreißers und die Zeile im Arbeitsblatt, die den Ausreißer enthält.

Methode

Nullhypothese	Alle Datenwerte stammen aus derselben normalverteilten Grundgesamtheit.
Alternativhypothese	Kleinster Datenwert ist ein Ausreißer
Signifikanzniveau	α = 0,05

Grubbs-Test

Variable	N	Mittelwert	StdAbw	Min	Max	G	p
Bruchfestigkeit	14	123,4	46,3	12,4	193,1	2,40	0,044

Ausreißer

Variable	Zeile	Ausreißer
Bruchfestigkeit	10	12,38

Wichtigste Ergebnisse: Zeile, Ausreißer

In diesen Ergebnissen ist der Wert des Ausreißers 12,38, und der Ausreißer befindet sich in Zeile 10.

Schritt 3: Ausreißer visuell identifizieren

Verwenden Sie das Diagramm der Ausreißer, um Ausreißer in den Daten visuell zu identifizieren. Wenn ein Ausreißer vorhanden ist, stellt Minitab diesen im Diagramm als rotes Quadrat dar. Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (so genannte Ausnahmebedingungen) zurückzuführen sind.

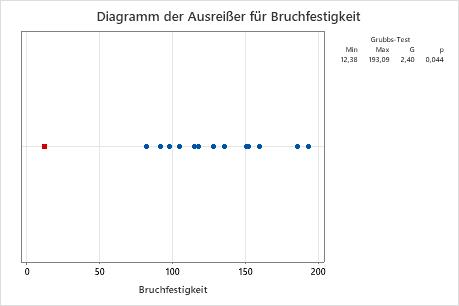
In diesem Diagramm der Ausreißer ist der kleinste Wert (12,38) ein Ausreißer.