In diesem Thema
Nullhypothese und Alternativhypothese
- Nullhypothese
- Die Nullhypothese besagt, dass alle Datenwerte aus derselben Normalverteilung stammen.
- Alternativhypothese
- Die Alternativhypothese besagt, dass entweder der kleinste oder der größte Datenwert ein Ausreißer ist.
Signifikanzniveau
Das Signifikanzniveau (als α oder Alpha bezeichnet) ist das maximal akzeptable Risiko, dass die Nullhypothese zurückgewiesen wird, wenn sie tatsächlich wahr ist (Fehler 1. Art). Der Standardwert ist 0,05.
Interpretation
Verwenden Sie das Signifikanzniveau, um zu entscheiden, ob die Nullhypothese (H0) zurückgewiesen oder nicht zurückgewiesen werden sollte. Wenn die Wahrscheinlichkeit, dass ein Ereignis eintritt, kleiner als das Signifikanzniveau ist, sind die Ergebnisse nach gängiger Interpretation statistisch signifikant, und Sie weisen H0 zurück.
- Wählen Sie ein höheres Signifikanzniveau wie 0,10, um möglicherweise vorhandene Differenzen mit größerer Gewissheit zu erkennen. Ein Qualitätstechniker vergleicht beispielsweise die Stabilität von neuen Kugellagern mit der Stabilität der derzeit verwendeten Kugellager. Der Techniker muss mit großer Sicherheit schlussfolgern können, dass die neuen Kugellager stabil sind, denn instabile Kugellager können schwere Unfälle nach sich ziehen. Er wählt ein Signifikanzniveau von 0,10, um mit größerer Sicherheit mögliche Differenzen in der Stabilität der Kugellager zu erkennen.
- Wählen Sie niedrigeres Signifikanzniveau wie 0,01, um mit größerer Sicherheit davon ausgehen zu können, dass nur tatsächlich vorhandene Differenzen erkannt werden. Ein Forscher in einem Pharmaunternehmen muss sich beispielsweise sehr sicher über die Behauptung sein, dass das neue Medikament des Unternehmens die Symptome signifikant reduziert. Er wählt ein Signifikanzniveau von 0,001, um mit größerer Sicherheit behaupten zu können, dass signifikante Differenzen hinsichtlich der Symptome tatsächlich vorhanden sind.
N
Der Stichprobenumfang (N) gibt die Gesamtzahl der Beobachtungen in der Stichprobe an.
Interpretation
Der Stichprobenumfang wirkt sich auf die Trennschärfe des Tests aus.
Bei größeren Stichprobenumfängen verfügt der Test in der Regel über eine höhere Trennschärfe zum Erkennen eines Ausreißers. Weitere Informationen finden Sie unter Was ist die Trennschärfe?.
Mittelwert
Der Mittelwert ist der Durchschnitt der Daten; hierbei handelt es sich um die Summe aller Beobachtungen dividiert durch die Anzahl der Beobachtungen.
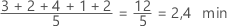
Interpretation
Verwenden Sie den Mittelwert, um die Stichprobe mit einem einzelnen Wert zu beschreiben, der das Zentrum der Daten darstellt. In vielen statistischen Analysen wird der Mittelwert als Standardmaß für die Lage der Datenverteilung verwendet.
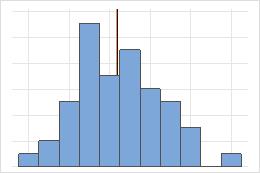
Symmetrisch
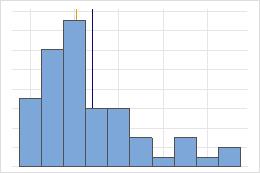
Nicht symmetrisch
Bei der symmetrischen Verteilung ähneln sich der Mittelwert (blaue Linie) und der Median (orangefarbene Linie) so sehr, dass die Linien nicht ohne weiteres unterschieden werden können. Die nicht symmetrische Verteilung ist jedoch rechtsschief.
StdAbw
Die Standardabweichung ist das am häufigsten verwendete Maß für die Streuung bzw. die Streubreite der Daten um den Mittelwert. Die Standardabweichung einer Grundgesamtheit wird häufig mit dem Zeichen σ (Sigma) angegeben, während mit s die Standardabweichung einer Stichprobe dargestellt wird. Eine zufällige oder natürliche Streuung eines Prozesses wird häufig auch als Rauschen bezeichnet.
Da die Standardabweichung in der gleichen Einheit wie die Daten angegeben wird, lässt sie sich in der Regel einfacher als die Varianz interpretieren.
Interpretation
Verwenden Sie die Standardabweichung, um die Streubreite der Daten um den Mittelwert zu ermitteln. Ein höherer Wert der Standardabweichung verweist auf eine größere Streubreite der Daten. Eine Faustregel für die Normalverteilung besagt, dass etwa 68 % der Werte innerhalb einer Standardabweichung vom Mittelwert, 95 % der Werte innerhalb zwei Standardabweichungen und 99,7 % der Werte innerhalb drei Standardabweichungen liegen.

Krankenhaus 1
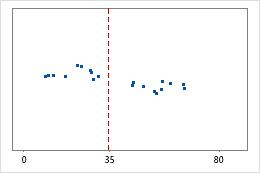
Krankenhaus 2
Zeit bis zur Entlassung in Krankenhäusern
Verwaltungsangestellte zeichnen die Zeit bis zur Entlassung von Patienten auf, die in der Notaufnahme zweier Krankenhäuser behandelt werden. Obwohl die durchschnittliche Zeit bis zur Entlassung in etwa identisch ist (35 Minuten), weichen die Standardabweichungen signifikant voneinander ab. Die Standardabweichung für Krankenhaus 1 beträgt etwa 6. Im Durchschnitt weicht die Zeit bis zur Entlassung eines Patienten um etwa 6 Minuten vom Mittelwert (gestrichelte Linie) ab. Die Standardabweichung für Krankenhaus 2 beträgt etwa 20. Im Durchschnitt weicht die Zeit bis zur Entlassung eines Patienten um ca. 20 Minuten vom Mittelwert (gestrichelte Linie) ab.
Maximum
Das Maximum ist der größte Datenwert.
In diesen Daten ist das Maximum 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretation
Verwenden Sie das Maximum, um einen möglichen Ausreißer oder einen Fehler bei der Dateneingabe zu identifizieren. Eine der einfachsten Möglichkeiten, um die Streubreite in den Daten zu ermitteln, ist ein Vergleich von Minimum und Maximum. Wenn der Wert des Maximums sehr hoch ist, selbst bei Berücksichtigung des Zentrums, der Streubreite und der Form der Daten, untersuchen Sie die Ursache für den Extremwert.
Minimum
Das Minimum ist der kleinste Datenwert.
In diesen Daten ist das Minimum 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretation
Verwenden Sie das Minimum, um einen möglichen Ausreißer oder einen Fehler bei der Dateneingabe zu identifizieren. Eine der einfachsten Möglichkeiten, um die Streubreite in den Daten zu ermitteln, ist ein Vergleich von Minimum und Maximum. Wenn der Wert des Minimums sehr niedrig ist, selbst bei Berücksichtigung des Zentrums, der Streubreite und der Form der Daten, untersuchen Sie die Ursache für den Extremwert.
Ausreißer
Ein Ausreißer ist eine ungewöhnlich große oder kleine Beobachtung. Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (so genannte Ausnahmebedingungen) zurückzuführen sind.
Zeile
Die Zeile im Arbeitsblatt, die den Ausreißer enthält. Minitab zeigt diesen Wert nur dann an, wenn ein Ausreißer vorhanden ist.
x[i] und x[N-i]
Wenn Sie einen der Dixon-Verhältnistests verwenden, zeigt Minitab zusätzlich zum Minimum und Maximum weitere Beobachtungen in der Testtabelle an. Der Wert in den Klammern gibt die Größe der Beobachtung relativ zu den anderen Werten an. Beispielsweise gibt „x[2]“ die zweitkleinste Beobachtung und „x[N-1]“ die zweitgrößte Beobachtung an.
G
Die Grubbs-Teststatistik (G) ist die Differenz zwischen dem Mittelwert der Stichprobe und entweder dem kleinsten oder dem größten Datenwert dividiert durch die Standardabweichung. Minitab verwendet die Grubbs-Teststatistik, um den p-Wert zu berechnen. Hierbei handelt es sich um die Wahrscheinlichkeit, dass die Nullhypothese verworfen wird, wenn diese wahr ist.
p
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Ein kleinerer p-Wert liefert stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Interpretation
Verwenden Sie den p-Wert, um zu ermitteln, ob ein Ausreißer vorhanden ist.
- p-Wert ≤ α: Es ist ein Ausreißer vorhanden (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass ein Ausreißer vorhanden ist. Versuchen Sie, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind.
- p-Wert > α: Es kann nicht gefolgert werden, dass ein Ausreißer vorhanden ist (H0 nicht verwerfen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück, da keine ausreichenden Hinweise für die Schlussfolgerung vorliegen, dass ein Ausreißer vorhanden ist. Vergewissern Sie sich, dass der Test über eine ausreichende Trennschärfe verfügt, um einen Ausreißer zu erkennen. Weitere Informationen finden Sie unter Erhöhen der Trennschärfe.
Diagramm der Ausreißer
Ein Diagramm der Ausreißer ähnelt einem Einzelwertdiagramm. Verwenden Sie das Diagramm der Ausreißer, um Ausreißer in den Daten visuell zu identifizieren. Wenn ein Ausreißer vorhanden ist, stellt Minitab diesen im Diagramm als rotes Quadrat dar. Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (so genannte Ausnahmebedingungen) zurückzuführen sind.
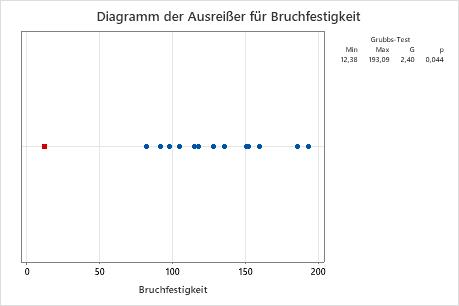
In diesen Ergebnissen ist der kleinste Wert (12,38) ein Ausreißer.
