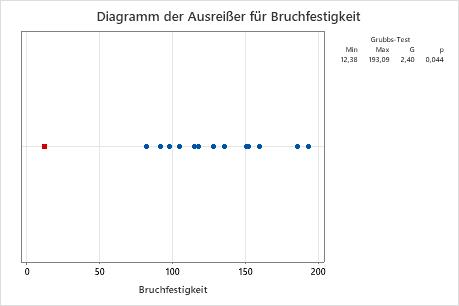
Ein Qualitätstechniker in einem Unternehmen für Holzstiele testet die Bruchfestigkeit einer Zufallsstichprobe von Besenstielen. Der Techniker erfasst die Kraft, die aufgewendet werden muss, um die einzelnen Stiele zu zerbrechen. Er erstellt ein Diagramm der Daten und stellt fest, dass ein Wert in der Stichprobe außergewöhnlich klein erscheint.
Der Techniker führt einen Test auf Ausreißer durch, um zu ermitteln, ob der kleinste Wert ein Ausreißer ist.
- Öffnen Sie die Beispieldaten Grifffestigkeit.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Variablen die Spalte Bruchfestigkeit ein.
- Klicken Sie auf Optionen.
- Wählen Sie im Feld Was möchten Sie ermitteln? (Alternativhypothese) den Wert Kleinster Datenwert ist ein Ausreißer aus.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
Der Mittelwert der Stichprobe beträgt 123,4. Die G-Statistik gibt an, dass der kleinste Datenwert 12,38 um 2,4 Standardabweichungen kleiner als der Mittelwert ist. Der p-Wert gibt an, dass die Wahrscheinlichkeit, einen derartig kleinen Mindestwert zu erhalten, wenn alle Werte tatsächlich aus derselben normalverteilten Grundgesamtheit stammen, lediglich 0,044 beträgt. Da der p-Wert 0,044 kleiner als das Signifikanzniveau (durch α oder Alpha bezeichnet) 0,05 ist, verwirft der Techniker die Nullhypothese und schlussfolgert, dass der kleinste Wert ein Ausreißer ist.
Der Techniker findet heraus, dass die Person, die die Daten eingegeben hat, versehentlich 12,38 anstelle von 123,8 eingegeben hat.
Methode
| Nullhypothese | Alle Datenwerte stammen aus derselben normalverteilten Grundgesamtheit. |
|---|---|
| Alternativhypothese | Kleinster Datenwert ist ein Ausreißer |
| Signifikanzniveau | α = 0,05 |
Grubbs-Test
| Variable | N | Mittelwert | StdAbw | Min | Max | G | p |
|---|---|---|---|---|---|---|---|
| Bruchfestigkeit | 14 | 123,4 | 46,3 | 12,4 | 193,1 | 2,40 | 0,044 |
Ausreißer
| Variable | Zeile | Ausreißer |
|---|---|---|
| Bruchfestigkeit | 10 | 12,38 |