In diesem Thema
Mittelwert
Ein häufig verwendetes Maß für das Zentrum einer Gruppe von Zahlen. Der Mittelwert wird auch als Durchschnitt bezeichnet. Es handelt sich um die Summe aller Beobachtungen dividiert durch die Anzahl der (nicht fehlenden) Beobachtungen.
Formel
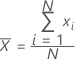
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
| N | Anzahl der nicht fehlenden Beobachtungen |
Standardabweichung (StdAbw)
Die Standardabweichung der Stichprobe bietet ein Maß für die Streubreite der Daten. Sie entspricht der Quadratwurzel der Varianz der Stichprobe.
Formel
, dann ist die Standardabweichung der Stichprobe:
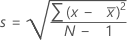
Notation
| Begriff | Beschreibung |
|---|---|
| x i | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
N
Anderson-Darling-Statistik (A2)
A2 misst die Fläche zwischen der Anpassungslinie (die auf der ausgewählten Verteilung basiert) und der verteilungsfreien Treppenfunktion (die auf den Diagrammpunkten basiert). Die Statistik ist eine quadrierte Distanz, die in den Randbereichen der Verteilung stärker gewichtet ist. Ein kleiner Anderson-Darling-Wert gibt an, dass die Verteilung besser auf die Daten passt.
Der Test auf Normalverteilung nach Anderson-Darling ist wie folgt definiert:
H0: Die Daten folgen einer Normalverteilung
H1: Die Daten folgen keiner Normalverteilung
Formel
Notation
| Begriff | Beschreibung |
|---|---|
| F(Yi) |  , wobei es sich um die inverse kumulative Verteilungsfunktion der Normalverteilung handelt |
| Yi | geordnete Daten |
Ryan-Joiner
Der Ryan-Joiner-Test liefert einen Korrelationskoeffizienten, der die Korrelation zwischen den Daten und den normalverteilten Werten der Daten angibt. Wenn der Korrelationskoeffizient nahe 1 liegt, liegen die Daten nahe am Wahrscheinlichkeitsnetz für Normalverteilung. Wenn er kleiner als der passende kritische Wert ist, verwerfen Sie die Nullhypothese, dass eine Normalverteilung vorliegt.
Formel
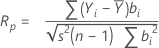
Notation
| Begriff | Beschreibung |
|---|---|
| Yi | geordnete Beobachtungen |
| bi | normalverteilte Werte der geordneten Daten |
| s2 | Stichprobenvarianz |
Kolmogorov-Smirnov
Formel
- H0: Die Daten folgen einer Normalverteilung
- H1: Die Daten folgen keiner Normalverteilung
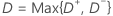
Notation
| Begriff | Beschreibung |
|---|---|
| D+ | Maxi {i / n – Z (i)} |
| D– | Maxi {Z (i) – (i – 1) / n)} |
| Z | F(X(i)) |
| F(x) | Wahrscheinlichkeitsfunktion der Normalverteilung |
| X(i) | Statistik für i-te Stelle einer Zufallsstichprobe, 1 ≤ i ≤ n |
| n | Stichprobenumfang |
p-Wert
Der p-Wert ist ein weiteres quantitatives Maß, mit dem das Ergebnis des Tests auf Normalverteilung angegeben wird. Ein kleiner p-Wert gibt an, dass die Nullhypothese falsch ist.
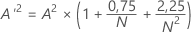
- Wenn 13 > A'2 > 0,600, dann p = exp(1,2937 – 5,709 * A'2 + 0,0186(A'2)2)
- Wenn 0,600 > A'2 > 0,340, dann p = exp(0,9177 – 4,279 * A'2 – 1,38(A'2)2)
- Wenn 0,340 > A'2 > 0,200, dann p = 1 – exp(–8,318 + 42,796 * A'2 – 59,938(A'2)2)
- Wenn A'2 <0,200, dann p = 1 – exp(–13,436 + 101,14 * A'2 – 223,73(A'2)2)
Diagrammpunkte
Je näher die Punkte an der Anpassungslinie liegen, desto besser ist im Allgemeinen die Anpassung. Minitab bietet zwei Maße für die Güte der Anpassung, mit denen die Anpassung der Verteilung an die Daten beurteilt werden kann.
Formel
| Verteilung | x-Koordinate | y-Koordinate |
|---|---|---|
| Normal | x | Φ–1 norm |
Notation
| Begriff | Beschreibung |
|---|---|
| Φ–1 norm | der für p von der inversen Verteilungsfunktion der Standardnormalverteilung zurückgegebene Wert |
Wahrscheinlichkeitsnetze
Die Eingabedaten werden als x-Werte dargestellt. Minitab berechnet die Wahrscheinlichkeit des Ereignisses, ohne eine Verteilung anzunehmen. Die y-Skala in der Grafik ähnelt der y-Skala auf Wahrscheinlichkeitspapier für Normalverteilung, bei der die Wahrscheinlichkeiten als gerade Linie dargestellt werden, als würden die Daten aus einer Normalverteilung stammen.
