Mittelwert
Der Mittelwert beschreibt die Stichprobe mit einem einzelnen Wert, der das Zentrum der Daten darstellt. Der Mittelwert wird als Durchschnitt der Daten berechnet; hierbei handelt es sich um die Summe aller Beobachtungen dividiert durch die Anzahl der Beobachtungen.
N
Der Stichprobenumfang (N) gibt die Gesamtzahl der Beobachtungen in der Stichprobe an.
Interpretation
Der Stichprobenumfang wirkt sich auf die Trennschärfe des Tests aus.
In der Regel erhält der Test durch einen größeren Stichprobenumfang eine höhere Trennschärfe, um eine Differenz zwischen den Stichprobendaten und der Normalverteilung zu erkennen. Das heißt, wenn tatsächlich eine Differenz vorhanden ist, erhöht sich mit einem größeren Stichprobenumfang die Wahrscheinlichkeit, diese zu erkennen.
StdAbw
Die Standardabweichung ist das am häufigsten verwendete Maß für die Streuung bzw. die Streubreite der Daten um den Mittelwert. Eine größere Stichproben-Standardabweichung verweist darauf, dass die Daten breiter um den Mittelwert gestreut sind.
AD
Mit der Anderson-Darling-Statistik für die Güte der Anpassung (AD) wird die Fläche zwischen der Anpassungslinie (die auf der Normalverteilung basiert) und der empirischen Verteilungsfunktion (die auf den Datenpunkten basiert) gemessen. Die Anderson-Darling-Statistik ist eine quadrierte Distanz, die in den Randbereichen der Verteilung stärker gewichtet ist.
Interpretation
Minitab verwendet die Anderson-Darling-Statistik, um den p-Wert zu berechnen. Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Ein kleinerer p-Wert liefert stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft. Größere Werte für die Anderson-Darling-Statistik geben an, dass die Daten der Normalverteilung nicht folgen.
KS
Bei dem Kolmogorov-Smirnov-Test wird die empirische kumulative Verteilungsfunktion (ECDF) Ihrer Stichprobendaten mit der Verteilung verglichen, die Sie erwarten würden, wenn die Daten normalverteilt wären.
Interpretation
Minitab verwendet die Kolmogorov-Smirnov-Statistik, um den p-Wert zu berechnen. Mit dem p-Wert wird die Wahrscheinlichkeit angegeben, eine Teststatistik (z. B. die Kolmogorov-Smirnov-Statistik) zu erhalten, die mindestens so extrem wie der anhand der Stichprobe berechnete Wert ist, wenn die Daten normalverteilt sind. Größere Werte für die Kolmogorov-Smirnov-Statistik geben an, dass die Daten der Normalverteilung nicht folgen.
RJ
Die Ryan-Joiner-Statistik misst, wie gut die Daten einer Normalverteilung folgen, indem die Korrelation zwischen den Daten und den normalverteilten Werten der Daten berechnet wird. Wenn der Korrelationskoeffizient nahe 1 liegt, ist die Grundgesamtheit wahrscheinlich normalverteilt. Dieser Test ähnelt dem Shapiro-Wilk-Test auf Normalverteilung.
Interpretation
Minitab verwendet die Ryan-Joiner-Statistik, um den p-Wert zu berechnen. Mit dem p-Wert wird die Wahrscheinlichkeit angegeben, eine Teststatistik (z. B. die Ryan-Joiner-Statistik) zu erhalten, die mindestens so extrem wie der anhand der Stichprobe berechnete Wert ist, wenn die Daten normalverteilt sind. Größere Werte für die Ryan-Joiner-Statistik geben an, dass die Daten der Normalverteilung nicht folgen.
p-Wert
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Ein kleinerer p-Wert liefert stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Interpretation
Verwenden Sie den p-Wert, um zu ermitteln, ob die Daten keiner Normalverteilung folgen.
- p-Wert ≤ α: Die Daten folgen keiner Normalverteilung (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass die Daten keiner Normalverteilung folgen.
- p-Wert > α: Es kann nicht gefolgert werden, dass die Daten keiner Normalverteilung folgen (H0 nicht verwerfen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen nicht genügend Anzeichen für die Schlussfolgerung vor, dass die Daten keiner Normalverteilung folgen.
Wahrscheinlichkeitsnetz
In einem Wahrscheinlichkeitsnetz wird eine geschätzte kumulative Verteilungsfunktion (CDF) aus der Stichprobe abgeleitet, indem der Wert jeder Beobachtung im Vergleich zur geschätzten kumulativen Wahrscheinlichkeit der Beobachtung aufgetragen wird.
Interpretation
Verwenden Sie ein Wahrscheinlichkeitsnetz, um zu veranschaulichen, wie gut Ihre Daten an die Normalverteilung angepasst sind.
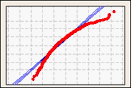
Rechtsschiefe Daten
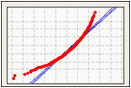
Linksschiefe Daten
Tipp
Verweilen Sie in Minitab mit dem Mauszeiger über der angepassten Verteilungslinie, um eine Tabelle der Perzentile und Werte abzurufen.
