In diesem Thema
Anderson-Darling-Statistik (A2)
A2 misst die Fläche zwischen der Anpassungslinie (die auf der ausgewählten Verteilung basiert) und der verteilungsfreien Treppenfunktion (die auf den Diagrammpunkten basiert). Die Statistik ist eine quadrierte Distanz, die in den Randbereichen der Verteilung stärker gewichtet ist. Ein kleiner Anderson-Darling-Wert gibt an, dass die Verteilung besser auf die Daten passt.
Der Test auf Normalverteilung nach Anderson-Darling ist wie folgt definiert:
H0: Die Daten folgen einer Normalverteilung
H1: Die Daten folgen keiner Normalverteilung
Formel
Notation
| Begriff | Beschreibung |
|---|---|
| F(Yi) |  , wobei es sich um die inverse kumulative Verteilungsfunktion der Normalverteilung handelt |
| Yi | geordnete Daten |
p-Wert für den Anderson-Darling-Test auf Normalverteilung
Der p-Wert ist ein quantitatives Maß, mit dem das Ergebnis des Anderson-Darling-Tests auf Normalverteilung angegeben wird. Ein kleiner p-Wert gibt an, dass die Nullhypothese falsch ist.
Wenn Sie A 2 kennen, können Sie den p-Wert berechnen.
Sei
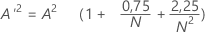
- Wenn 13 > A'2 > 0,600, dann p = exp(1,2937 - 5,709 * A'2 + 0,0186(A'2)2)
- Wenn 0,600 > A'2 > 0,340, dann p = exp(0,9177 - 4,279 * A'2 – 1,38(A'2)2)
- Wenn 0,340 > A'2 > 0,200, dann p = 1 – exp(–8,318 + 42,796 * A'2 – 59,938(A'2)2)
- Wenn A'2 < 0,200, dann p = 1 – exp(–13,436 + 101,14 * A'2 – 223,73(A'2)2)
N nicht fehlend (N)
Die Anzahl der nicht fehlenden Werte in der Stichprobe.
Standardabweichung (StdAbw)
Die Standardabweichung der Stichprobe bietet ein Maß für die Streubreite der Daten. Sie entspricht der Quadratwurzel der Varianz der Stichprobe.
Formel
, dann ist die Standardabweichung der Stichprobe:
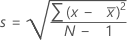
Notation
| Begriff | Beschreibung |
|---|---|
| x i | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
Varianz
Die Varianz ist ein Maß der Streuung der Daten um ihren Mittelpunkt. Die Varianz ist gleich dem Quadrat der Standardabweichung.
Formel
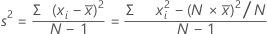
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
Schiefe
Schiefe ist ein Maß für Asymmetrie. Ein negativer Wert gibt eine Schiefe nach links an, und ein positiver Wert gibt eine Schiefe nach rechts an. Ein Nullwert deutet nicht unbedingt auf Symmetrie hin.
Formel
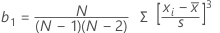
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
| s | Standardabweichung der Stichprobe |
Kurtosis
Die Kurtosis ist ein Maß dafür, wie weit eine Verteilung von der Normalverteilung abweicht. Ein positiver Wert deutet in der Regel darauf hin, dass sich die Verteilung durch eine steilere Wölbung als die Normalverteilung auszeichnet. Ein negativer Wert deutet darauf hin, dass die Verteilung eine flachere Wölbung als die Normalverteilung aufweist.
Formel
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
| s | Standardabweichung der Stichprobe |
Mittelwert
Ein häufig verwendetes Maß für das Zentrum einer Gruppe von Zahlen. Der Mittelwert wird auch als Durchschnitt bezeichnet. Es handelt sich um die Summe aller Beobachtungen dividiert durch die Anzahl der (nicht fehlenden) Beobachtungen.
Formel
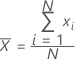
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
| N | Anzahl der nicht fehlenden Beobachtungen |
Minimum
Der kleinste Wert im Datensatz.
Maximum
Der größte Wert in Ihrem Datensatz.
1. Quartil (Q1)
25 % Ihrer Stichprobenbeobachtungen sind kleiner oder gleich dem Wert des 1. Quartils. Daher wird das 1. Quartil auch als das 25. Perzentil bezeichnet.
Formel
Notation
| Begriff | Beschreibung |
|---|---|
| y | auf ganze Zahl abgeschnittener Wert von w |
| w |  |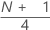
| z | abgeschnittener Nachkommaanteil von w |
| xj | j-te Beobachtung in der Liste von Stichprobendaten, von der kleinsten zur größten geordnet |
Hinweis
Wenn w eine ganze Zahl ist: y = w, z = 0 und Q1 = xy.
Median
Der Stichproben-Median liegt in der Mitte der Daten: Mindestens die Hälfte der Beobachtungen sind kleiner oder gleich und mindestens die Hälfte sind größer oder gleich dem Stichproben-Median.
Angenommen, eine Spalte enthält N Werte. Um den Median zu berechnen, ordnen Sie die Datenwerte zunächst vom kleinsten zum größten an. Wenn N eine ungerade Zahl ist, handelt es sich bei dem Stichproben-Median um den Wert in der Mitte. Wenn N eine gerade Zahl ist, handelt es sich bei dem Stichproben-Median um den Durchschnitt der beiden mittleren Werte.
Beispiel: Wenn N = 5 und die Daten x1, x2, x3, x4 und x5 vorliegen, ist der Median = x3.
Wenn N = 6 und die geordneten Daten x1, x2, x3, x4, x5 und x6 vorliegen:
wobei x3 und x4 die dritte und vierte Beobachtung sind.
3. Quartil (Q3)
75 % Ihrer Stichprobenbeobachtungen sind kleiner oder gleich dem Wert des dritten Quartils. Daher wird das dritte Quartil auch als das 75. Perzentil bezeichnet.
Formel
Notation
| Begriff | Beschreibung |
|---|---|
| y | auf ganze Zahl abgeschnittener Wert von w |
| w |
 |
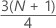| z | abgeschnittener Nachkommaanteil von w |
| xj | j-te Beobachtung in der Liste von Stichprobendaten, von der kleinsten zur größten geordnet |
Hinweis
Wenn w eine ganze Zahl ist: y = w, z = 0 und Q3 = xy.
Konfidenzintervall für den Mittelwert
Formel
Notation
| Begriff | Beschreibung |
|---|---|
 | Mittelwert |
| s | Standardabweichung der Stichprobe |
| N | Anzahl nicht fehlender Beobachtungen |
| t N, α | Inverse kumulative Wahrscheinlichkeit einer t-Verteilung mit N – 1 Freiheitsgraden bei 1 – α/2; α = 1 – Konfidenzniveau/100 |
Konfidenzintervall für den Median
Minitab verwendet die nichtlineare Interpolation zur Berechnung des Konfidenzintervalls für den tatsächlichen Median 1. Diese Methode ist eine sehr gute Approximation für eine Vielzahl von symmetrischen Verteilungen, darunter die Normalverteilung, die Cauchy-Verteilung und die Gleichverteilung. Beispiele für nichtsymmetrische Verteilungen zeigen angemessene Ergebnisse, die immer wesentlich genauer sind als bei der linearen Interpolation.
Konfidenzintervall für die Standardabweichung
Minitab berechnet ein (1 – α)100%-Konfidenzintervall für die Standardabweichung der Grundgesamtheit σ. Das Konfidenzintervall ist sehr empfindlich gegenüber der Annahme, dass die Daten normalverteilt sind. Selbst geringfügige Abweichungen von der Normalverteilung können zu einem irreführenden Konfidenzintervall führen.
Formel
Das Konfidenzintervall reicht von:
Notation
| Begriff | Beschreibung |
|---|---|
| s | Standardabweichung |
| N | Anzahl nicht fehlender Beobachtungen |
| χ2N, α | inverse kumulative Wahrscheinlichkeit einer χ2-Verteilung mit N Freiheitsgraden bei 1 – α / 2; α = 1 – Konfidenzniveau / 100 |
