In diesem Thema
Schritt 1: Zentrum der Daten beschreiben
Verwenden Sie den Mittelwert, um die Stichprobe mit einem einzelnen Wert zu beschreiben, der das Zentrum der Daten darstellt. In vielen statistischen Analysen wird der Mittelwert als Standardmaß für die Lage der Datenverteilung verwendet.
Der Median ist ein weiteres Maß für die Lage der Verteilung der Daten. Der Median wird im Allgemeinen weniger von Ausreißern beeinflusst als der Mittelwert. Die Hälfte der Datenwerte ist größer als der Median, und die Hälfte der Datenwerte ist kleiner als der Median.
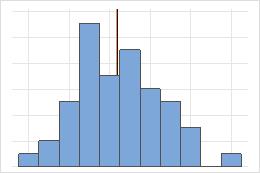
Symmetrisch
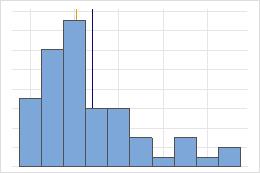
Nicht symmetrisch
Bei der symmetrischen Verteilung ähneln sich der Mittelwert (blaue Linie) und der Median (orangefarbene Linie) so sehr, dass die Linien nicht ohne weiteres unterschieden werden können. Die nicht symmetrische Verteilung ist jedoch rechtsschief.
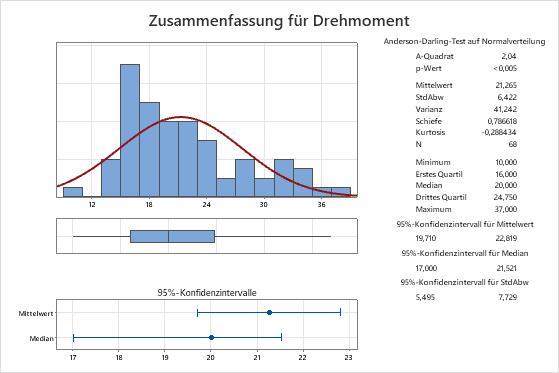
Wichtigste Ergebnisse: Mittelwert und Median
In diesen Ergebnissen beträgt der Mittelwert des Drehmoments, der erforderlich ist, um die Verschlusskappe einer Zahnpastatube abzuschrauben, 21,265, und der Median des Drehmoments ist 20. Die Daten scheinen eine Rechtsschiefe aufzuweisen. Dies erklärt, warum der Mittelwert größer als der Median ist.
Schritt 2: Ein Konfidenzintervall für den Mittelwert, den Median und die Standardabweichung bestimmen
Das Konfidenzintervall ist ein Bereich wahrscheinlicher Werte für den Parameter der Grundgesamtheit. Ein 95%-Konfidenzniveau gibt beispielsweise an, dass bei einer Entnahme von 100 Zufallsstichproben aus der Grundgesamtheit die Konfidenzintervalle für voraussichtlich ca. 95 der Stichproben den Parameter der Grundgesamtheit enthalten.

Wichtigste Ergebnisse: Konfidenzintervall für Mittelwert, Konfidenzintervall für Median, Konfidenzintervall für StdAbw
- Der Mittelwert der Grundgesamtheit für die Drehmoment-Messwerte liegt zwischen 19,710 und 22,819.
- Der Median der Grundgesamtheit für die Drehmoment-Messwerte liegt zwischen 17 und 21,521.
- Die Standardabweichung der Grundgesamtheit für die Drehmoment-Messwerte liegt zwischen 5,495 und 7,729.
Schritt 3: Form und Streubreite der Datenverteilung auswerten
Verwenden Sie das Histogramm und das Boxplot, um die Form und Streubreite der Daten auszuwerten und potenzielle Ausreißer zu identifizieren.
Untersuchen der Streubreite der Daten, um zu ermitteln, ob die Daten schief sind
Wenn Daten schief sind, befinden sich die meisten Daten im oberen oder unteren Teil der Grafik. Schiefe ist häufig am einfachsten mit einem Histogramm oder Boxplot zu erkennen.
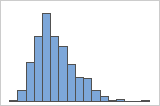
Rechtsschief
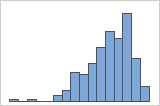
Linksschief
Das Histogramm mit rechtsschiefen Daten zeigt Wartezeiten. Der Großteil der Wartezeiten ist relativ kurz, nur wenige Wartezeiten sind lang. Das Histogramm mit linksschiefen Daten zeigt Daten zu Ausfallzeiten. Einige Elemente fallen sofort aus, deutlich mehr Elemente fallen später aus.
Identifizieren von Ausreißern
Ausreißer, d. h. Daten, die sich weit entfernt von den anderen Datenwerten befinden, können starke Auswirkungen auf die Ergebnisse Ihrer Analyse haben. Häufig lassen sich Ausreißer am einfachsten in einem Boxplot erkennen.
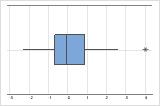
In einem Boxplot werden Ausreißer mit einem Asterisk (*) gekennzeichnet.
Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (so genannte Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse. Weitere Informationen finden Sie unter Identifizieren von Ausreißern.
Suchen nach multimodalen Daten
Multimodale Daten weisen mehrere Spitzen auf, die auch als Modalwerte bezeichnet werden. Multimodale Daten deuten oftmals darauf hin, dass wichtige Variablen noch nicht berücksichtigt wurden.
Wenn Sie über zusätzliche Informationen verfügen, die es Ihnen ermöglichen, die Beobachtungen in Gruppen zu gliedern, können Sie anhand dieser Informationen eine Gruppierungsvariable anlegen. Dann können Sie die Grafik mit den Gruppen erstellen, um zu ermitteln, ob die Gruppierungsvariable die Spitzen in den Daten erklärt.
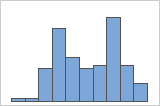
Einfach
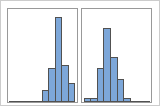
Mit Gruppen
Ein Manager in einer Bank erfasst beispielsweise Daten zu Wartezeiten und erstellt ein einfaches Histogramm. Das Histogramm weist zwei Spitzen auf. Nach eingehenderen Untersuchungen stellt der Manager fest, dass die Wartezeiten für Kunden, die Schecks einlösen, kürzer als die Wartezeiten für Kunden sind, die einen Eigenheimkredit beantragen. Der Manager fügt eine Gruppierungsvariable für den Besuchszweck hinzu und erstellt dann ein Histogramm mit Gruppen.
