Interpretieren der wichtigsten Ergebnisse für Test auf Poisson-Verteilung

Führen Sie die folgenden Schritte aus, um einen Test auf Poisson-Verteilung zu interpretieren. Zu den wichtigsten Ausgaben zählen der p-Wert und mehrere Grafiken.

In diesem Thema

Schritt 1: Ermitteln, ob die Daten keiner Poisson-Verteilung folgen
Schritt 2: Differenz zwischen den beobachteten und den erwarteten Werten für jede Kategorie untersuchen

Schritt 1: Ermitteln, ob die Daten keiner Poisson-Verteilung folgen

Um zu ermitteln, ob die Daten keiner Poisson-Verteilung folgen, vergleichen Sie den p-Wert mit dem Signifikanzniveau (α). In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko der Schlussfolgerung, dass die Daten keiner Poisson-Verteilung folgen, wenn sie tatsächlich einer Poisson-Verteilung folgen, von 5 %.

p-Wert ≤ α: Die Daten folgen keiner Poisson-Verteilung (H₀ verwerfen): Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass die Daten keiner Poisson-Verteilung folgen.
p-Wert > α: Es kann nicht gefolgert werden, dass die Daten keiner Poisson-Verteilung folgen (H₀ nicht verwerfen): Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück, da nicht genügend Anzeichen für die Schlussfolgerung vorliegen, dass die Daten keiner Poisson-Verteilung folgen.

Methode

Häufigkeiten in Beobachtet

Deskriptive Statistik

N	Mittelwert
300	0,536667

Beobachtete und erwartete Anzahlen für Fehler

Fehler	Poisson-Wahrscheinlichkeit	Beobachtete Anzahl	Erwartete Anzahl	Beitrag zu Chi-Quadrat
0	0,584694	213	175,408	8,056
1	0,313786	41	94,136	29,993
2	0,084199	18	25,260	2,086
>=3	0,017321	28	5,196	100,072

Chi-Quadrat-Test

Nullhypothese	H₀: Die Daten folgen einer Poisson-Verteilung.
Alternativhypothese	H₁: Die Daten folgen keiner Poisson-Verteilung.

DF	Chi-Quadrat	p-Wert
2	140,208	0,000

Wichtigstes Ergebnis: p-Wert

In diesen Ergebnissen besagt die Nullhypothese, dass die Daten einer Poisson-Verteilung folgen. Da der p-Wert 0,000 beträgt und somit kleiner als 0,05 ist, weisen Sie die Nullhypothese zurück. Sie können folgern, dass die Daten nicht aus einer Poisson-Verteilung stammen.

Schritt 2: Differenz zwischen den beobachteten und den erwarteten Werten für jede Kategorie untersuchen

Verwenden Sie ein Balkendiagramm der beobachteten und erwarteten Werte, um für jede Kategorie zu ermitteln, ob die Anzahl der beobachteten Werte von der Anzahl der erwarteten Werte abweicht. Größere Unterschiede zwischen den beobachteten und den erwarteten Werten geben an, dass die Daten nicht einer Poisson-Verteilung folgen.

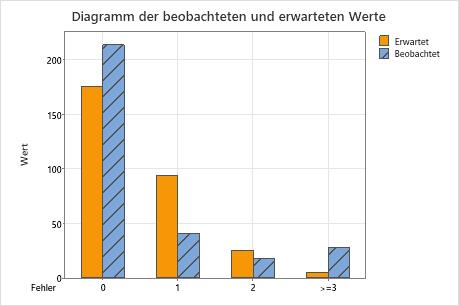
Dieses Balkendiagramm zeigt, dass die beobachteten Werte für 0 Fehler, 1 Fehler und mehr als 3 Fehler von den erwarteten Werten abweichen. Das Balkendiagramm bestätigt also visuell, was der p-Wert angibt, nämlich dass die Daten nicht einer Poisson-Verteilung folgen.