Ein Qualitätstechniker in einem Unternehmen für Unterhaltungselektronik möchte feststellen, ob die Anzahl der Fehler pro Fernsehgerät einer Poisson-Verteilung folgen. Der Techniker wählt nach dem Zufallsprinzip 300 Fernsehgeräte aus und zeichnet die Anzahl der Fehler pro Fernsehgerät auf.
- Öffnen Sie die Beispieldaten Fernsehgerätefehler.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Variable die Spalte Fehler ein.
- Geben Sie im Feld Häufigkeitenvariable: (optional) die Spalte Beobachtet ein.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
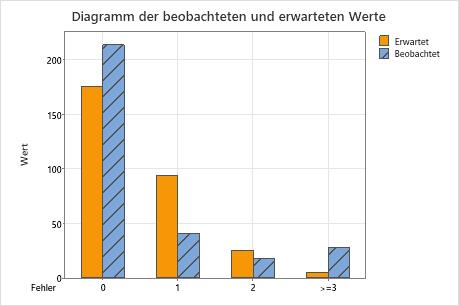
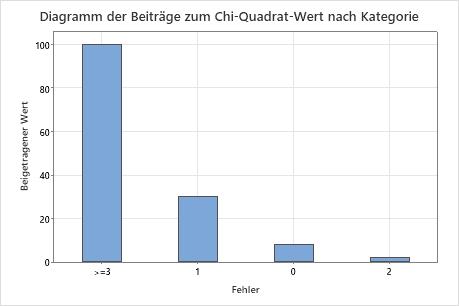
Die Nullhypothese besagt, dass die Daten einer Poisson-Verteilung folgen. Da der p-Wert 0,000 beträgt und somit niedriger als das Signifikanzniveau 0,05 ist, verwirft der Ingenieur die Nullhypothese und folgert, dass die Daten nicht einer Poisson-Verteilung folgen. Die Grafiken zeigen, dass die Differenz zwischen den beobachteten und den erwarteten Werten für die Kategorien 1 und 
3 hoch ist, und dass die Kategorie 3 den größten Beitrag zur Chi-Quadrat-Statistik liefert.
Methode
| Häufigkeiten in Beobachtet |
|---|
Deskriptive Statistik
| N | Mittelwert |
|---|---|
| 300 | 0,536667 |
Beobachtete und erwartete Anzahlen für Fehler
| Fehler | Poisson-Wahrscheinlichkeit | Beobachtete Anzahl | Erwartete Anzahl | Beitrag zu Chi-Quadrat |
|---|---|---|---|---|
| 0 | 0,584694 | 213 | 175,408 | 8,056 |
| 1 | 0,313786 | 41 | 94,136 | 29,993 |
| 2 | 0,084199 | 18 | 25,260 | 2,086 |
| >=3 | 0,017321 | 28 | 5,196 | 100,072 |
Chi-Quadrat-Test
| Nullhypothese | H₀: Die Daten folgen einer Poisson-Verteilung. |
|---|---|
| Alternativhypothese | H₁: Die Daten folgen keiner Poisson-Verteilung. |
| DF | Chi-Quadrat | p-Wert |
|---|---|---|
| 2 | 140,208 | 0,000 |
