Ein Qualitätsingenieur möchte sicherstellen, dass die Verschlusskappen auf Shampooflaschen ordnungsgemäß festgedreht sind. Wenn die Verschlusskappen zu lose aufgedreht sind, können Sie beim Transport abfallen. Wenn sie zu fest aufgedreht sind, lassen sich die Flaschen möglicherweise zu schwer öffnen. Das Soll-Drehmoment zum Festziehen der Verschlusskappen beträgt 18. Der Ingenieur zieht eine Zufallsstichprobe von 68 Flaschen und prüft, welches Drehmoment benötigt wird, um die Verschlusskappen zu entfernen.
Im Rahmen der anfänglichen Untersuchung analysiert der Ingenieur die deskriptive Statistik der Drehmoment-Messwerte, um die Verteilung der Daten für die einzelnen Maschinen zu ermitteln.
- Öffnen Sie die Beispieldaten Kappendrehmoment.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Variablen die Spalte Drehmoment ein.
- Geben Sie im Feld Nach Variablen (optional) die Spalte Maschine ein.
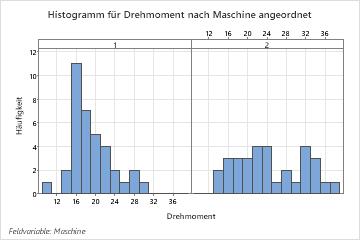
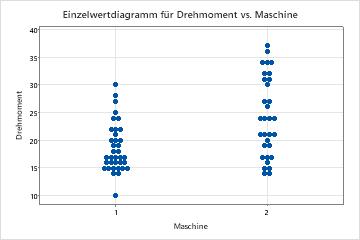
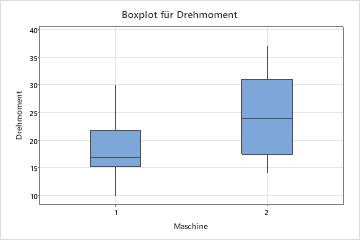
- Klicken Sie auf die Schaltfläche Grafiken, und aktivieren Sie dann Histogramm der Daten, Einzelwertdiagramm und Boxplot der Daten.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
Der Mittelwert des Drehmoments für Maschine 1 ist näher am Sollwert 18 als der Mittelwert des Drehmoments für Maschine 2. Das zum Abdrehen von Verschlusskappen erforderliche mittlere Drehmoment für Maschine 1 ist 18,667, und das zum Abdrehen von Verschlusskappen erforderliche mittlere Drehmoment für Maschine 2 ist 24,19. Die Verteilung der Daten von Maschine 1 ist außerdem weniger variabel. Die Standardabweichung für Maschine 1 beträgt 4,395, für Maschine 2 beträgt sie 7,12.
Die Grafiken zeigen außerdem eine Differenz des mittleren Drehmoments für die beiden Maschinen. Um zu bestimmen, ob eine signifikante Differenz der Mittelwerte der Grundgesamtheiten vorliegt, könnte der Ingenieur einen t-Test bei zwei Stichproben durchführen.
Statistik
| Variable | Maschine | N | N* | Mittelwert | SE des Mittelwerts | StdAbw | Minimum | Q1 | Median | Q3 |
|---|---|---|---|---|---|---|---|---|---|---|
| Drehmoment | 1 | 36 | 0 | 18,6667 | 0,732467 | 4,39480 | 10 | 15,25 | 17 | 21,75 |
| 2 | 32 | 0 | 24,1875 | 1,25839 | 7,11852 | 14 | 17,5 | 24 | 31 |
| Variable | Maschine | Maximum |
|---|---|---|
| Drehmoment | 1 | 30 |
| 2 | 37 |