In diesem Thema
Pearson-Korrelationskoeffizient
Formel
Misst den Grad der linearen Beziehung zwischen zwei Variablen. Der Korrelationskoeffizient kenn einen Wert zwischen −1 und +1 annehmen. Wenn eine Variable zunimmt, während die andere abnimmt, ist der Korrelationskoeffizient negativ. Wenn die beiden Variablen umgekehrt dazu neigen gemeinsam anzusteigen, ist der Korrelationskoeffizient positiv.
Für die Variablen x und y:
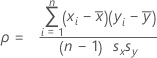
Notation
| Begriff | Beschreibung |
|---|---|
 | Mittelwert der Stichprobe für die erste Variable |
| sx | Standardabweichung der Stichprobe für die erste Variable |
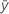 | Mittelwert der Stichprobe für die zweite Variable |
| sy | Standardabweichung der Stichprobe für die zweite Variable |
| n | Anzahl der Beobachtungen |
Konfidenzintervalle für Korrelation nach Pearson
Das beidseitige (1− α)100%-Konfidenzintervall für ρ ist (ρU, ρO), wobei die Untergrenze ρU und die Obergrenze ρO wie folgt angegeben werden:

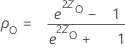
Dabei gilt Folgendes:


Notation
| Begriff | Beschreibung |
|---|---|
| r | Geschätzte Stichprobenkorrelation nach Pearson für die unbekannte Korrelation ρ |
| ρ | Korrelationskoeffizient |
| n | Anzahl der Beobachtungen |
Spearman-Korrelationskoeffizient
Zum Berechnen des Spearman-Korrelationskoeffizienten und des p-Werts führen Sie eine Pearson-Korrelation für die nach Rangfolge geordneten Daten durch. Die Rangfolgen gebundener Antworten sind die durchschnittlichen Rangfolgen der Bindungen. In der folgenden Tabelle werden die Rangfolgen für zwei Stichproben von Daten gezeigt.
| C1 | C2 | C3 | C4 |
|---|---|---|---|
| A | Rang A | B | Rang B |
| 45 | 4 | 23 | 1 |
| 78 | 6 | 25 | 3 |
| 24 | 3 | 25 | 3 |
| 51 | 5 | 25 | 3 |
| 13 | 1,5 | 34 | 6 |
| 13 | 1,5 | 30 | 5 |
Der Korrelationskoeffizient nach Spearman zwischen A und B ist −0,678, und der p-Wert beträgt 0,139. Diese Werte sind identisch mit dem Koeffizienten und p-Wert aus einer Pearson-Korrelation für die Werte in Rangfolge A und B.
Minitab schließt für eine oder beide Variablen Zeilen von der Berechnung aus, die einen fehlenden Wert enthalten. Beide Spalten müssen dieselbe Anzahl von Zeilen enthalten.
Konfidenzintervalle für die Korrelation nach Spearman
Das beidseitige (1− α)100%-Konfidenzintervall für ρ ist (ρU, ρO), wobei für die Untergrenze ρU und die Obergrenze ρO Folgendes gilt:
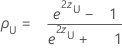

Dabei gilt Folgendes:


Bonnett und Wright (2000) empfehlen die folgende Korrektur des Standardfehlers:

Notation
| Begriff | Beschreibung |
|---|---|
| r | Geschätzte Stichprobenkorrelation nach Spearman für die unbekannte Korrelation ρ |
| ρ | Korrelationskoeffizient |
| n | Anzahl der Zeilen ohne fehlende Daten für das Variablenpaar |
p-Wert
Die Hypothesen für einen Test auf eine Korrelation von 0 lauten wie folgt:
H0: ρ = 0 im Vergleich zu H1: ρ ≠ 0, wobei ρ der Korrelationskoeffizient nach Pearson oder der Korrelationskoeffizient nach Spearman zwischen einem Paar von Variablen ist.
Formel
Die Teststatistiken für den Korrelationskoeffizienten nach Pearson und für den Korrelationskoeffizienten nach Spearman werden anhand der gleichen Formel berechnet:

Der p-Wert ist 2 × P(T > t), wobei T einer t-Verteilung mit n – 2 Freiheitsgraden folgt.
Notation
| Begriff | Beschreibung |
|---|---|
| r | Korrelationskoeffizient der Stichprobe |
| n | Anzahl der Beobachtungen |
