In diesem Thema
Schritt 1: Untersuchen der Beziehungen zwischen Variablen in einem Matrixplot
Verwenden Sie ein Matrixplot, um die Beziehungen zwischen zwei stetigen Variablen zu untersuchen. Außerdem können Sie nach Ausreißern in den Beziehungen suchen. Ausreißer können die Ergebnisse für den Korrelationskoeffizienten nach Pearson erheblich beeinflussen.
Bestimmen Sie, ob die Beziehungen linear, monoton oder keines von beiden sind. Im Folgenden finden Sie Beispiele für die verschiedenen Formen, die von den Korrelationskoeffizienten beschrieben werden. Der Korrelationskoeffizient nach Pearson eignet sich für lineare Formen. Der Korrelationskoeffizient nach Spearman eignet sich für monotone Formen.

Keine Beziehung
Die Punkte liegen zufällig im Diagramm. Dies deutet darauf hin, dass keine lineare Beziehung zwischen den Variablen besteht.
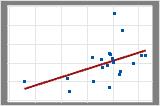
Moderate positive Beziehung
Einige Punkte liegen dicht an der Linie, andere jedoch weit davon entfernt. Dies weist lediglich auf eine mittlere lineare Beziehung zwischen den Variablen hin.
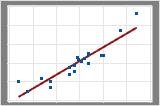
Starke positive Beziehung
Die Punkte folgen der Linie eng, was auf eine starke lineare Beziehung zwischen den Variablen hindeutet. Die Beziehung ist positiv, da beim Ansteigen der einen Variable die andere ebenfalls ansteigt.
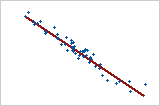
Starke negative Beziehung
Die Punkte folgen der Linie eng, was auf eine starke negative Beziehung zwischen den Variablen hindeutet. Die Beziehung ist negativ, da beim Ansteigen der einen Variable die andere fällt.
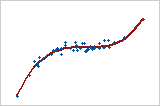
Monoton
In einer monotonen Beziehung bewegen sich die Variablen tendenziell in dieselbe relative Richtung, aber nicht zwangsläufig mit einer konstanten Rate. In einer linearen Beziehung bewegen sich die Variablen mit einer konstanten Rate in dieselbe Richtung. Dieses Diagramm zeigt, dass beide Variablen gleichzeitig zunehmen, jedoch nicht mit der gleichen Rate. Diese Beziehung ist monoton, aber nicht linear. Der Korrelationskoeffizient nach Pearson für diese Daten ist 0,843, doch der Korrelationskoeffizient nach Spearman ist mit 0,948 höher.
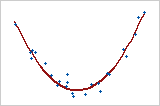
Gekrümmt quadratisch
In diesem Beispiel wird eine gekrümmte Beziehung veranschaulicht. Obwohl die Beziehung zwischen den Variablen stark ist, liegt der Korrelationskoeffizient nahe null. Die Beziehung ist weder linear noch monoton.
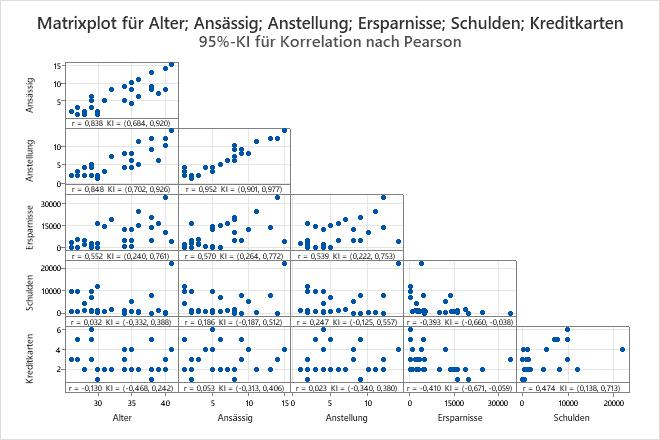
Wichtigstes Ergebnis: Matrixplot
- Eine starke positive lineare Beziehung besteht zwischen Beschäftigung und Wohnort.
- Eine schwache negative lineare Beziehung besteht zwischen Kreditkarten und Ersparnisse.
- Schulden weist anscheinend einen Ausreißer auf, der untersucht werden sollte.
Schritt 2: Untersuchen der Korrelationskoeffizienten zwischen Variablen
Verwenden Sie den Pearson-Korrelationskoeffizienten, um Stärke und Richtung der linearen Beziehung zwischen zwei stetigen Variablen zu untersuchen.
- Stärke
-
Der Korrelationskoeffizient kann einen Wert zwischen −1 und +1 annehmen. Je größer der Absolutwert des Koeffizienten, desto stärker ist die Beziehung zwischen den Variablen.
Bei der Pearson-Korrelation gibt ein Absolutwert von 1 eine perfekte lineare Beziehung an. Eine Korrelation nahe 0 gibt an, dass keine lineare Beziehung zwischen den Variablen vorliegt. - Richtung
-
Das Vorzeichen des Koeffizienten gibt die Richtung der Beziehung an. Wenn beide Variablen gleichzeitig ansteigen oder abfallen, ist der Koeffizient positiv, und die Linie, die die Korrelation darstellt, hat eine Aufwärtsneigung. Wenn eine Variable tendenziell ansteigt, während die andere abfällt, ist der Korrelationskoeffizient negativ, und die Linie, die die Korrelation darstellt, hat eine Abwärtsneigung.
- Aus der Korrelation allein kann nicht gefolgert werden, dass Änderungen an einer Variablen die Ursache von Änderungen an einer anderen Variablen darstellen. Nur bei ordnungsgemäß kontrollierten Experimenten kann bestimmt werden, ob eine kausale Beziehung vorliegt.
- Der Pearson-Korrelationskoeffizient ist gegenüber Extremwerten sehr empfindlich. Ein einzelner Wert, der erheblich von den anderen Werten in einem Datensatz abweicht, kann den Wert des Koeffizienten beträchtlich verändern. Sie sollten versuchen, die Ursache für Extremwerte zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
- Ein kleiner Korrelationskoeffizient nach Pearson bedeutet nicht, dass zwischen den Variablen keine Beziehung besteht. Die Variablen können möglicherweise eine nichtlineare Beziehung aufweisen.
Methode
| Korrelationstyp | Pearson |
|---|---|
| Anzahl der verwendeten Zeilen | 30 |
Korrelationen
| Alter | Ansässig | Anstellung | Ersparnisse | Schulden | |
|---|---|---|---|---|---|
| Ansässig | 0,838 | ||||
| Anstellung | 0,848 | 0,952 | |||
| Ersparnisse | 0,552 | 0,570 | 0,539 | ||
| Schulden | 0,032 | 0,186 | 0,247 | -0,393 | |
| Kreditkarten | -0,130 | 0,053 | 0,023 | -0,410 | 0,474 |
Wichtigstes Ergebnis: Korrelation nach Pearson
- Wohnort und Alter: 0,838
- Beschäftigung und Alter: 0,848
- Beschäftigung und Wohnort: 0,952
- Schulden und Ersparnisse: −0,393
- Kreditkarten und Alter: −0,130
- Kreditkarten und Ersparnisse: −0,410
