In diesem Thema
Korrelationen nach Pearson
Die Korrelationsmatrix zeigt die Korrelationswerte, die den Grad der linearen Beziehung zwischen den einzelnen Variablenpaaren messen. Die Korrelation kann Werte von –1 bis +1 annehmen. Wenn zwei Variablen tendenziell gleichzeitig zu- bzw. abnehmen, ist der Korrelationswert positiv. Wenn eine Variable steigt und die andere gleichzeitig fällt, ist der Korrelationswert negativ.
Interpretation
Mit der Korrelationsmatrix können Sie die Stärke und Richtung der Beziehung zwischen zwei Variablen untersuchen. Hohe, positive Korrelationswerte weisen darauf hin, dass die Variablen dasselbe Merkmal messen. Wenn die Items nicht stark korrelieren, messen sie möglicherweise verschiedene Merkmale oder sind nicht klar definiert.
Korrelationen
| Alter | Ansässig | Anstellung | Ersparnisse | Schulden | |
|---|---|---|---|---|---|
| Ansässig | 0,838 | ||||
| Anstellung | 0,848 | 0,952 | |||
| Ersparnisse | 0,552 | 0,570 | 0,539 | ||
| Schulden | 0,032 | 0,186 | 0,247 | -0,393 | |
| Kreditkarten | -0,130 | 0,053 | 0,023 | -0,410 | 0,474 |
- Wohnort und Alter: 0,838
- Beschäftigung und Alter: 0,848
- Beschäftigung und Wohnort: 0,952
- Schulden und Ersparnisse: −0,393
- Kreditkarten und Alter: −0,130
- Kreditkarten und Ersparnisse: −0,410
Korrelationen nach Spearman
Verwenden Sie den Spearman-Korrelationskoeffizienten, um Stärke und Richtung der monotonen Beziehung zwischen zwei stetigen oder ordinalen Variablen zu untersuchen. In einer monotonen Beziehung bewegen sich die Variablen tendenziell in dieselbe relative Richtung, aber nicht zwangsläufig mit einer konstanten Rate. Zum Berechnen der Spearman-Korrelation bildet Minitab eine Rangfolge der Rohdaten. Dann berechnet Minitab den Korrelationskoeffizienten der nach Rangfolge sortierten Daten.
- Festigkeit
-
Der Korrelationskoeffizient kann einen Wert zwischen −1 und +1 annehmen. Je größer der Absolutwert des Koeffizienten, desto stärker ist die Beziehung zwischen den Variablen.
Bei der Spearman-Korrelation gibt ein Absolutwert von 1 an, dass die nach Rangfolge geordneten Daten perfekt linear sind. Beispiel: Bei einer Spearman-Korrelation von -1 ist der höchste Wert von Variable A dem niedrigsten Wert von Variable B zugeordnet, der zweithöchste Wert von Variable A ist dem zweitniedrigsten Wert von Variable B zugeordnet usw.
- Richtung
-
Das Vorzeichen des Koeffizienten gibt die Richtung der Beziehung an. Wenn beide Variablen gleichzeitig ansteigen oder abfallen, ist der Koeffizient positiv, und die Linie, die die Korrelation darstellt, hat eine Aufwärtsneigung. Wenn eine Variable tendenziell ansteigt, während die andere abfällt, ist der Korrelationskoeffizient negativ, und die Linie, die die Korrelation darstellt, hat eine Abwärtsneigung.
Die folgenden Diagramme zeigen Daten mit spezifischen Werten des Spearman-Korrelationskoeffizienten, um verschiedene Muster in der Stärke und Richtung der Beziehungen zwischen Variablen zu veranschaulichen.

Keine Beziehung: Spearmans Rho = 0
Die Punkte liegen zufällig im Diagramm. Dies deutet darauf hin, dass keine Beziehung zwischen den Variablen besteht.
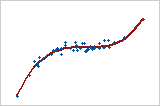
Starke positive Beziehung: Spearmans Rho = 0,948
Die Punkte folgen der Linie eng, was auf eine starke Beziehung zwischen den Variablen hindeutet. Die Beziehung ist positiv, da die Variablen gleichzeitig steigen.

Starke negative Beziehung: Spearmans Rho = -1,0
Die Punkte folgen der Linie eng, was auf eine starke Beziehung zwischen den Variablen hindeutet. Die Beziehung ist negativ, da beim Ansteigen der einen Variable die andere fällt.
Aus der Korrelation allein kann nicht gefolgert werden, dass Änderungen an einer Variablen die Ursache von Änderungen an einer anderen Variablen darstellen. Nur bei ordnungsgemäß kontrollierten Experimenten kann bestimmt werden, ob eine kausale Beziehung vorliegt.
Interpretation
Korrelationen
| Alter | Ansässig | Anstellung | Ersparnisse | Schulden | |
|---|---|---|---|---|---|
| Ansässig | 0,824 | ||||
| Anstellung | 0,830 | 0,912 | |||
| Ersparnisse | 0,570 | 0,571 | 0,496 | ||
| Schulden | -0,198 | -0,142 | -0,056 | -0,605 | |
| Kreditkarten | -0,179 | 0,069 | 0,036 | -0,480 | 0,353 |
Paarweise Korrelationen nach Spearman
| Stichprobe 1 | Stichprobe 2 | N | Korrelation | 95%-KI für ρ | p-Wert |
|---|---|---|---|---|---|
| Ansässig | Alter | 30 | 0,824 | (0,624; 0,922) | 0,000 |
| Anstellung | Alter | 30 | 0,830 | (0,636; 0,926) | 0,000 |
| Ersparnisse | Alter | 30 | 0,570 | (0,236; 0,783) | 0,001 |
| Schulden | Alter | 30 | -0,198 | (-0,524; 0,178) | 0,293 |
| Kreditkarten | Alter | 30 | -0,179 | (-0,508; 0,197) | 0,345 |
| Anstellung | Ansässig | 30 | 0,912 | (0,798; 0,963) | 0,000 |
| Ersparnisse | Ansässig | 30 | 0,571 | (0,237; 0,784) | 0,001 |
| Schulden | Ansässig | 30 | -0,142 | (-0,479; 0,232) | 0,454 |
| Kreditkarten | Ansässig | 30 | 0,069 | (-0,300; 0,419) | 0,719 |
| Ersparnisse | Anstellung | 30 | 0,496 | (0,144; 0,737) | 0,005 |
| Schulden | Anstellung | 30 | -0,056 | (-0,408; 0,311) | 0,768 |
| Kreditkarten | Anstellung | 30 | 0,036 | (-0,328; 0,392) | 0,849 |
| Schulden | Ersparnisse | 30 | -0,605 | (-0,804; -0,283) | 0,000 |
| Kreditkarten | Ersparnisse | 30 | -0,480 | (-0,726; -0,124) | 0,007 |
| Kreditkarten | Schulden | 30 | 0,353 | (-0,020; 0,639) | 0,056 |
In diesen Ergebnissen ist die Spearman-Korrelation zwischen Wohnort und Alter 0,824, was darauf hinweist, dass eine positive Beziehung zwischen den Variablen besteht. Das Konfidenzintervall für Rho erstreckt sich von 0,624 bis 0,922. Der p-Wert ist gleich 0,000, was darauf verweist, dass die Beziehung bei α = 0,05 statistisch signifikant ist.
Die Spearman-Korrelation zwischen Schulden und Ersparnissen ist -0,605, zwischen Kreditkarten und Ersparnissen beträgt sie -0,480. Die Beziehung zwischen diesen Variablen ist negativ, was darauf hindeutet, dass bei steigenden Schulden und zunehmender Anzahl von Kreditkarten die Ersparnisse abnehmen.
Verwendete Zeilen
Die Anzahl der verwendeten Zeilen wird in der Regressionstabelle angezeigt. Dies ist die Anzahl der Datenzeilen, einschließlich der fehlenden Werte.
Liegen fehlende Werte vor, entspricht die Anzahl der verwendeten Zeilen nicht dem tatsächlichen Stichprobenumfang, der in der Berechnung der Konfidenzintervalle verwendet wird.
Konfidenzintervalle für die Korrelation
Das Konfidenzintervall ist ein Bereich wahrscheinlicher Werte für die Korrelationskoeffizienten. Da die Stichproben zufällig sind, ist es unwahrscheinlich, dass zwei Stichproben aus einer Grundgesamtheit identische Konfidenzintervalle ergeben. Wenn Sie die Stichprobennahme jedoch viele Male wiederholen, enthält ein bestimmter Prozentsatz der resultierenden Konfidenzintervalle oder -grenzen den unbekannten Korrelationskoeffizienten. Der Prozentsatz dieser Konfidenzintervalle oder -grenzen, die den Korrelationskoeffizienten enthalten, stellt das Konfidenzniveau des Intervalls dar.
Ein 95%-Konfidenzniveau gibt beispielsweise an, dass bei einer Entnahme von 100 Zufallsstichproben aus der Grundgesamtheit die Konfidenzintervalle für voraussichtlich ca. 95 der Stichproben den Korrelationskoeffizienten enthalten.
Eine Obergrenze ist der Wert, der wahrscheinlich größer als die Differenz der Grundgesamtheit ist. Eine Untergrenze ist der Wert, der wahrscheinlich kleiner als die Differenz der Grundgesamtheit ist.
Die Konfidenzintervalle für die Pearson-Korrelation sind empfindlich gegenüber Abweichungen von der Normalverteilung der zugrunde liegenden bivariaten Verteilung. Wenn die Daten von der Normalverteilung abweichen, können die Konfidenzintervalle ungeachtet der Größe des Stichprobenumfangs ungenau sein.
Die Konfidenzintervalle für Spearman-Korrelationen basieren auf einer Rangfolge, und sie sind weniger empfindlich gegenüber Abweichungen von der angenommenen zugrunde liegenden bivariaten Verteilung.
Interpretation
Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihrer Ergebnisse beurteilen. Bestimmen Sie anhand Ihrer Fachkenntnisse, ob das Konfidenzintervall Werte umfasst, die in der jeweiligen Situation von praktischer Signifikanz sind. Wenn das Intervall zu breit und damit nicht hilfreich ist, erwägen Sie, den Stichprobenumfang zu vergrößern. Weitere Informationen finden Sie unter Möglichkeiten zum Erhöhen der Genauigkeit des Konfidenzintervalls.
Paarweise Korrelationen nach Pearson
| Stichprobe 1 | Stichprobe 2 | N | Korrelation | 95%-KI für ρ | p-Wert |
|---|---|---|---|---|---|
| Ansässig | Alter | 30 | 0,838 | (0,684; 0,920) | 0,000 |
| Anstellung | Alter | 30 | 0,848 | (0,702; 0,926) | 0,000 |
| Ersparnisse | Alter | 30 | 0,552 | (0,240; 0,761) | 0,002 |
| Schulden | Alter | 30 | 0,032 | (-0,332; 0,388) | 0,865 |
| Kreditkarten | Alter | 30 | -0,130 | (-0,468; 0,242) | 0,494 |
| Anstellung | Ansässig | 30 | 0,952 | (0,901; 0,977) | 0,000 |
| Ersparnisse | Ansässig | 30 | 0,570 | (0,264; 0,772) | 0,001 |
| Schulden | Ansässig | 30 | 0,186 | (-0,187; 0,512) | 0,326 |
| Kreditkarten | Ansässig | 30 | 0,053 | (-0,313; 0,406) | 0,779 |
| Ersparnisse | Anstellung | 30 | 0,539 | (0,222; 0,753) | 0,002 |
| Schulden | Anstellung | 30 | 0,247 | (-0,125; 0,557) | 0,189 |
| Kreditkarten | Anstellung | 30 | 0,023 | (-0,340; 0,380) | 0,906 |
| Schulden | Ersparnisse | 30 | -0,393 | (-0,660; -0,038) | 0,032 |
| Kreditkarten | Ersparnisse | 30 | -0,410 | (-0,671; -0,059) | 0,024 |
| Kreditkarten | Schulden | 30 | 0,474 | (0,138; 0,713) | 0,008 |
In diesen Ergebnissen besteht eine positive lineare Korrelation von 0,838 zwischen Wohnort und Alter. Sie können sich zu 95 % sicher sein, dass der Korrelationskoeffizient der Grundgesamtheit zwischen 0,684 und 0,920 liegt. Im Allgemeinen ist das Konfidenzintervall bei einer stärkeren Korrelation schmaler. Zwischen Kreditkarten und Alter besteht beispielsweise eine schwache Korrelation, und das 95%-Konfidenzintervall erstreckt sich von -0,468 bis 0,242.
p-Wert
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Ein kleinerer p-Wert liefert stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Interpretation
Bestimmen Sie mit Hilfe des p-Werts, ob der Korrelationskoeffizient statistisch signifikant ist.
- p-Wert ≤ α: Die Korrelation ist statistisch signifikant (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück. Sie können schlussfolgern, dass die Korrelation statistisch signifikant ist. Bestimmen Sie anhand Ihres Fachwissens, ob die Differenz praktisch signifikant ist. Weitere Informationen finden Sie unter Statistische und praktische Signifikanz.
- p-Wert > α: Die Korrelation ist statistisch nicht signifikant (H0 nicht verwerfen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen keine hinreichenden Hinweise darauf vor, dass die Korrelation statistisch signifikant ist.
Die p-Wert-Verfahren für die Korrelation nach Pearson und die Korrelation nach Spearman sind gegenüber Abweichungen von der Normalverteilung robust. Die p-Werte sind im Allgemeinen genau für n ≥ 25, ungeachtet der übergeordneten Grundgesamtheit der Stichprobe.
Paarweise Korrelationen nach Pearson
| Stichprobe 1 | Stichprobe 2 | N | Korrelation | 95%-KI für ρ | p-Wert |
|---|---|---|---|---|---|
| Ansässig | Alter | 30 | 0,838 | (0,684; 0,920) | 0,000 |
| Anstellung | Alter | 30 | 0,848 | (0,702; 0,926) | 0,000 |
| Ersparnisse | Alter | 30 | 0,552 | (0,240; 0,761) | 0,002 |
| Schulden | Alter | 30 | 0,032 | (-0,332; 0,388) | 0,865 |
| Kreditkarten | Alter | 30 | -0,130 | (-0,468; 0,242) | 0,494 |
| Anstellung | Ansässig | 30 | 0,952 | (0,901; 0,977) | 0,000 |
| Ersparnisse | Ansässig | 30 | 0,570 | (0,264; 0,772) | 0,001 |
| Schulden | Ansässig | 30 | 0,186 | (-0,187; 0,512) | 0,326 |
| Kreditkarten | Ansässig | 30 | 0,053 | (-0,313; 0,406) | 0,779 |
| Ersparnisse | Anstellung | 30 | 0,539 | (0,222; 0,753) | 0,002 |
| Schulden | Anstellung | 30 | 0,247 | (-0,125; 0,557) | 0,189 |
| Kreditkarten | Anstellung | 30 | 0,023 | (-0,340; 0,380) | 0,906 |
| Schulden | Ersparnisse | 30 | -0,393 | (-0,660; -0,038) | 0,032 |
| Kreditkarten | Ersparnisse | 30 | -0,410 | (-0,671; -0,059) | 0,024 |
| Kreditkarten | Schulden | 30 | 0,474 | (0,138; 0,713) | 0,008 |
In diesen Ergebnissen liegen viele p-Werte unter dem Signifikanzniveau von 0,05, was darauf hinweist, dass die Korrelationskoeffizienten nach Pearson statistisch signifikant sind.
Hinweis
Gelegentlich kann der p-Wert aufgrund extremer Datenpunkte klein sein, während das Konfidenzintervall sehr breit ist. Bei Kreditkarten und Schulden beispielsweise ist das 95%-KI sehr breit, der p-Wert ist jedoch klein. Bei einer Betrachtung des Matrixplots stellen Sie fest, dass ein extremer Datenpunkt vorhanden ist.
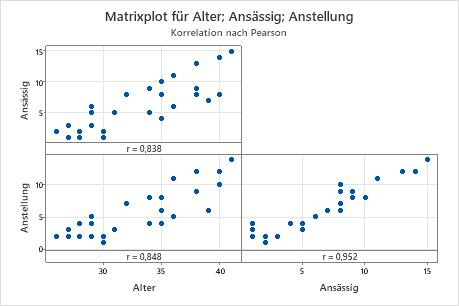
Matrixplot
Ein Matrixplot ist ein Feld von Streudiagrammen. Jedes Streudiagramm in der Matrix stellt die Werte für ein Item-Paar auf der x- und der y-Achse dar.
Interpretation
Verwenden Sie das Diagramm, um die Beziehung zwischen den einzelnen Kombinationen von Variablen visuell auszuwerten. Die Beziehungen können linear, monoton oder weder linear noch monoton sein. Sie können das Matrixplot auch verwenden, um nach Ausreißern zu suchen, die die Ergebnisse erheblich beeinflussen können. Weitere Informationen zu den Arten von Beziehungen finden Sie unter Lineare, nichtlineare und monotone Beziehungen.
Dieses Matrixplot weist darauf hin, dass alle Item-Paare eine positive lineare Beziehung aufweisen.