Eine Bank benötigt acht Angaben von Kreditantragstellern: Einkommen, Bildungsniveau, Alter, Ansässigkeitsdauer am gegenwärtigen Wohnsitz, Anstellungsdauer beim gegenwärtigen Arbeitgeber, Ersparnisse, Schulden und Anzahl der Kreditkarten. Ein Bankangestellter möchte diese Daten analysieren, um die beste Möglichkeit zu ermitteln, sie zu gruppieren und in Berichten darzustellen. Der Angestellte erfasst diese Angaben für 30 Kreditantragsteller.
Der Bankangestellte untersucht anhand der Korrelationen nach Pearson die Stärke und Richtung der linearen Beziehungen zwischen den einzelnen Variablenpaaren.
- Öffnen Sie die Beispieldaten Kreditanträge.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Variablen die Spalten Alter Ansässig Anstellung Ersparnisse Schulden 'Kreditkarten' ein.
- Klicken Sie auf Grafiken.
- Wählen Sie in Auf Plot darzustellende Statistiken die Option Korrelationen und Intervalle aus.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
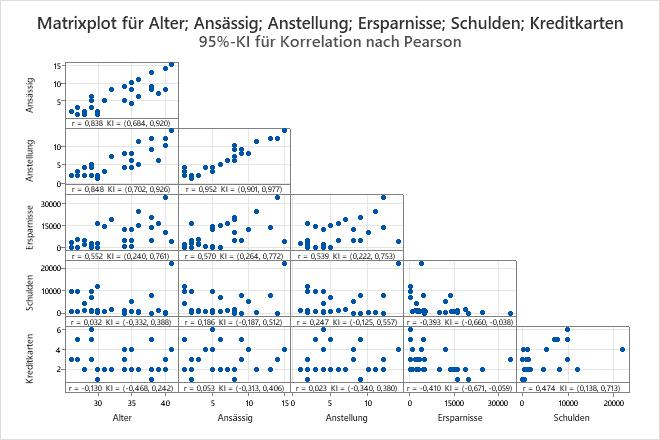
- Der höchste Korrelationskoeffizient nach Pearson liegt zwischen Beschäftigung und Wohnort vor. Der Wert 0,952 stellt eine positive Beziehung zwischen den Variablen dar. Mit zunehmendem Wert für Beschäftigung nimmt auch der Wert für Wohnort zu. Das 95%-Konfidenzintervall erstreckt sich von 0,901 bis 0,977.
- Der Korrelationskoeffizient nach Pearson zwischen Kreditkarten und Ersparnisse beträgt –0,410. Mit zunehmender Anzahl von Kreditkarten nehmen die Ersparnisse tendenziell ab. Das 95%-Konfidenzintervall reicht von –0,671 bis –0,059.
Sie können das Matrixplot auch verwenden, um nach Ausreißern zu suchen, die die Ergebnisse erheblich beeinflussen können. Zeile 6 enthält beispielsweise einen extremen Datenpunkt, der die Korrelation zwischen Variablen beeinflussen kann. Ein Beispiel hierfür ist im Diagramm für Schulden und Alter ersichtlich.
Im Allgemeinen ist das Konfidenzintervall bei einer stärkeren Korrelation schmaler. Zwischen Kreditkarten und Alter besteht beispielsweise eine schwache Korrelation, und das 95%-Konfidenzintervall erstreckt sich von -0,468 bis 0,242.
Methode
| Korrelationstyp | Pearson |
|---|---|
| Anzahl der verwendeten Zeilen | 30 |
Korrelationen
| Alter | Ansässig | Anstellung | Ersparnisse | Schulden | |
|---|---|---|---|---|---|
| Ansässig | 0,838 | ||||
| Anstellung | 0,848 | 0,952 | |||
| Ersparnisse | 0,552 | 0,570 | 0,539 | ||
| Schulden | 0,032 | 0,186 | 0,247 | -0,393 | |
| Kreditkarten | -0,130 | 0,053 | 0,023 | -0,410 | 0,474 |
