Ein Gesundheitsberater möchte die Bewertungen der Zufriedenheit von Patienten für zwei Krankenhäuser vergleichen. Der Berater erfasst die Bewertungen von 20 Patienten pro Krankenhaus.
Der Berater führt einen Test auf Varianzen bei zwei Stichproben durch, um zu bestimmen, ob sich die Standardabweichungen der Patientenbewertungen für die zwei Krankenhäuser voneinander unterscheiden.
- Öffnen Sie die Beispieldaten Krankenhausvergleich.MWX.
- Wählen Sie aus.
- Wählen Sie in der Dropdownliste die Option Beide Stichproben befinden sich in einer Spalte aus.
- Geben Sie im Feld Stichproben die Spalte Bewertung ein.
- Geben Sie im Feld Stichproben-IDs die Spalte Krankenhaus ein.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
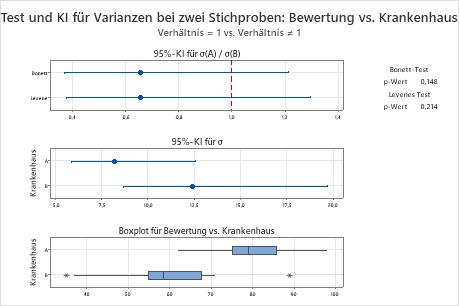
Die Nullhypothese besagt, dass das Verhältnis zwischen den Standardabweichungen 1 beträgt. Da beide p-Werte größer als Signifikanzniveau (als α oder Alpha bezeichnet) 0,05 sind, verwirft der Berater die Nullhypothese nicht. Der Berater verfügt über zu wenig Anzeichen, um zu schlussfolgern, dass sich die Standardabweichungen der Krankenhäuser unterscheiden.
Methode
| σ₁: Standardabweichung von Bewertung, wenn Krankenhaus = A |
|---|
| σ₂: Standardabweichung von Bewertung, wenn Krankenhaus = B |
| Verhältnis: σ₁/σ₂ |
| Die Bonett- und die Levene-Methode sind für alle stetigen Verteilungen gültig. |
Deskriptive Statistik
| Krankenhaus | N | StdAbw | Varianz | 95%-KI für σ |
|---|---|---|---|---|
| A | 20 | 8,183 | 66,958 | (5,893; 12,597) |
| B | 20 | 12,431 | 154,537 | (8,693; 19,709) |
Verhältnis der Standardabweichungen
| Geschätztes Verhältnis | 95%-KI für Verhältnis unter Verwendung von Bonett | 95%-KI für Verhältnis unter Verwendung von Levene |
|---|---|---|
| 0,658241 | (0,372; 1,215) | (0,378; 1,296) |
Test
| Nullhypothese | H₀: σ₁ / σ₂ = 1 |
|---|---|
| Alternativhypothese | H₁: σ₁ / σ₂ ≠ 1 |
| Signifikanzniveau | α = 0,05 |
| Methode | Teststatistik | DF1 | DF2 | p-Wert |
|---|---|---|---|---|
| Bonett | 2,09 | 1 | 0,148 | |
| Levene | 1,60 | 1 | 38 | 0,214 |