In diesem Thema
Konfidenzintervall (KI)
Formel
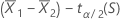bis 
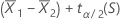
Notation
| Begriff | Beschreibung |
|---|---|
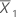 | Mittelwert der ersten Stichprobe |
 | Mittelwert der zweiten Stichprobe |
| tα/2 | inverse kumulative Wahrscheinlichkeit einer t-Verteilung bei 1 – α/2 |
| α | 1 - Konfidenzniveau/100 |
| s | Standardabweichung der Stichprobe wie für die Teststatistik berechnet |
t-Wert
Formel
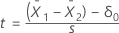
hängt von der Varianzannahme ab.
- Ungleiche Varianzen
-
Bei der Annahme von ungleichen Varianzen ist die Standardabweichung der Stichprobe
gleich:
Die Freiheitsgrade sind:
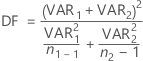
Falls erforderlich, schneidet Minitab die Freiheitsgrade auf eine ganze Zahl ab. Dies ist ein konservativerer Ansatz als das Runden.
- Gleiche Varianzen
-
Bei der Annahme von gleichen Varianzen wird die gemeinsame Varianz durch die zusammengefasste Varianz geschätzt:
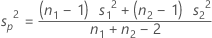Die Standardabweichung
wird geschätzt durch:
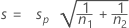
Die Freiheitsgrade der Teststatistik sind:
DF = n1 + n2 – 2
Notation
| Begriff | Beschreibung |
|---|---|
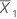 | Mittelwert der ersten Stichprobe |
 | Mittelwert der zweiten Stichprobe |
| s | Standardabweichung der Stichprobe  |
| δ0 | Hypothesendifferenz zwischen den zwei Mittelwerten der Grundgesamtheiten |
| s1 | Stichproben-Standardabweichung der ersten Stichprobe |
| s2 | Stichproben-Standardabweichung der zweiten Stichprobe |
| n1 | Stichprobenumfang der ersten Stichprobe |
| n2 | Stichprobenumfang der zweiten Stichprobe |
| VAR1 |  |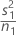
| VAR2 |  |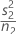
Berechnen der zusammengefassten Standardabweichung
Angenommen, C1 enthält die Antwortvariable, und C3 enthält den Mittelwert für jede Faktorstufe. Beispiel:
| C1 | C2 | C3 |
|---|---|---|
| Antwort | Faktor | Mittelwert |
| 18,95 | 1 | 14,5033 |
| 12,62 | 1 | 14,5033 |
| 11,94 | 1 | 14,5033 |
| 14,42 | 2 | 10,5567 |
| 10,06 | 2 | 10,5567 |
| 7,19 | 2 | 10,5567 |
- Wählen Sie aus.
- Geben Sie im Feld Ergebnis speichern in Variable die Spalte C4 ein.
- Geben Sie im Feld Ausdruck den Ausdruck SQRT((SUM((C1 - C3)**2)) / (Gesamtzahl der Beobachtungen - Anzahl der Gruppen)) ein. Im vorherigen Beispiel wäre der Ausdruck für die zusammengefasste Standardabweichung: SQRT((SUM(('Antwort' - 'Mittelwert')**2)) / (6 - 2))
Minitab speichert den Wert 3,75489.
p-Wert
Formel
Die Berechnung für den p-Wert hängt von der Alternativhypothese ab.
| Alternativhypothese | p-Wert |
|---|---|
 |
 |
 |
 |
 |
 |
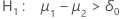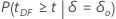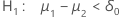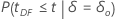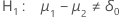- Ungleiche Varianzen
-
Bei der Annahme von ungleichen Varianzen sind die Freiheitsgrade:
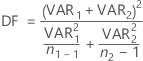
Falls erforderlich, schneidet Minitab die Freiheitsgrade auf eine ganze Zahl ab. Dies ist ein konservativerer Ansatz als das Runden.
- Gleiche Varianzen
-
Bei der Annahme gleicher Varianzen sind die Freiheitsgrade der Teststatistik:
DF = n1 + n2 – 2
Notation
| Begriff | Beschreibung |
|---|---|
| μ1 | Mittelwert der Grundgesamtheit der ersten Stichprobe |
| μ1 | Mittelwert der Grundgesamtheit der zweiten Stichprobe |
| n1 | Stichprobenumfang der ersten Stichprobe |
| n2 | Stichprobenumfang der zweiten Stichprobe |
| δ0 | Hypothesendifferenz zwischen den zwei Mittelwerten der Grundgesamtheiten |
| t | t-Statistik der Stichprobendaten |
| t | eine Zufallsvariable aus der t-Verteilung mit DF Freiheitsgraden |
| VAR1 |  |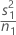
| VAR2 |  |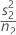
