Methoden und Formeln für Ereignisrate in Poisson-Modellen, 2 Stichproben

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Statistik
Hypothesentest für eine Differenz zwischen Raten für die Normal-Approximation
Hypothesentest für eine Differenz zwischen Raten für die exakte Methode
Hypothesentest für eine Differenz zwischen Raten für die Methode der zusammengefassten Raten
Hypothesentest für eine Differenz der Mittelwerte für die Methode der Normal-Approximation
Hypothesentest für eine Differenz der Mittelwerte für die exakte Methode
Hypothesentest für eine Differenz der Mittelwerte für die Methode der zusammengefassten Mittelwerte
Konfidenzintervall für die Differenz der Raten
Konfidenzgrenzen für die Differenz der Raten
Konfidenzintervall für die Differenz der Mittelwerte
Konfidenzgrenzen für die Differenz der Mittelwerte

Statistik

Minitab generiert die folgende deskriptive Statistik aus Ihrer Stichprobe. Minitab zeigt nur dann einen Mittelwert an, wenn Sie den „Beobachtungsumfang“ vom Standardwert 1 in einen anderen Wert ändern.

Begriff	Beschreibung
Ereignisrate für Stichprobe i

Begriff	Beschreibung
mittlere Ereignishäufigkeit in Stichprobe i

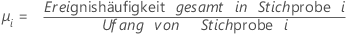Hypothesentest für eine Differenz zwischen Raten für die Normal-Approximation

Formel

Der Test mit einer Normal-Approximation basiert auf der folgenden z-Statistik, die gemäß der Nullhypothese annähernd eine Standardnormalverteilung aufweist:

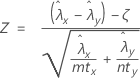
Minitab verwendet die folgenden Gleichungen für den p-Wert der jeweiligen Alternativhypothesen:

Notation

Begriff	Beschreibung
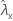	beobachteter Wert der Rate für Stichprobe X
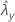	beobachteter Wert der Rate für Stichprobe Y
ζ	wahrer Wert der Differenz zwischen den Raten der Grundgesamtheiten von zwei Stichproben
ζ₀	Hypothesenwert der Differenz zwischen den Raten der Grundgesamtheiten von zwei Stichproben
m	Stichprobenumfang von Stichprobe X
n	Stichprobenumfang von Stichprobe Y
t_x	Beobachtungsumfang von Stichprobe X
t_y	Beobachtungsumfang von Stichprobe Y

Hypothesentest für eine Differenz zwischen Raten für die exakte Methode

Formel

Wenn die hypothetische Differenz gleich 0 ist, verwendet Minitab ein exaktes Verfahren, um die folgende Nullhypothese testen:

H₀: ζ = λ_x – λ_y = 0 oder H₀: λ_x = λ_y

Das exakte Verfahren basiert auf der folgenden Tatsache unter der Annahme, dass die Nullhypothese wahr ist:

S | W ~ Binomial(w, p)

Dabei gilt Folgendes:

W = S + U

Minitab verwendet die folgenden Gleichungen für den p-Wert der jeweiligen Alternativhypothesen:

H₁: ζ > 0: p-Wert = P(S ≥ s | w = s + u, p = p₀)
H₁: ζ < 0: p-Wert = P(S ≤ s | w = s + u, p = p₀)
H₁: ζ ≠ 0:
- wenn P(S ≤ s | w = s + u, p = p₀) ≤ 0,5 oder P(S ≥ s | w = s + u, p = p₀) ≤ 0,5
  dann ist der p-Wert = 2 × Min {P(S ≤ s | w = s + u, p = p₀), P(S ≥ s | w = s + u, p = p₀)}
- andernfalls ist der p-Wert = 1,0.

Dabei gilt Folgendes:

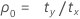
Notation

Begriff	Beschreibung
	beobachteter Wert der Rate für Stichprobe X
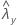	beobachteter Wert der Rate für Stichprobe Y
λ_x	wahrer Wert der Rate für die Grundgesamtheit X
λ_y	wahrer Wert der Rate für die Grundgesamtheit Y
ζ	wahrer Wert der Differenz zwischen den Raten der Grundgesamtheiten von zwei Stichproben
t_x	Beobachtungsumfang von Stichprobe X
t_y	Beobachtungsumfang von Stichprobe Y
m	Stichprobenumfang von Stichprobe X
n	Stichprobenumfang von Stichprobe Y

Hypothesentest für eine Differenz zwischen Raten für die Methode der zusammengefassten Raten

Wenn Sie eine Differenz von null mit der folgenden Nullhypothese testen, können Sie eine zusammengefasste Rate für beide Stichproben verwenden:

Formel

Das Verfahren der zusammengefassten Rate basiert auf der folgenden z-Statistik, die gemäß der folgenden Nullhypothese annähernd eine Standardnormalverteilung aufweist:

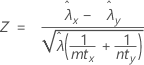
Dabei gilt Folgendes:

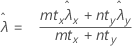
Minitab verwendet die folgenden Gleichungen für den p-Wert der jeweiligen Alternativhypothesen:

Notation

Begriff	Beschreibung
	beobachteter Wert der Rate für Stichprobe X
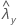	beobachteter Wert der Rate für Stichprobe Y
λ_x	wahrer Wert der Rate für die Grundgesamtheit X
λ_y	wahrer Wert der Rate für die Grundgesamtheit Y
ζ	wahrer Wert der Differenz zwischen den Raten der Grundgesamtheiten von zwei Stichproben
m	Stichprobenumfang von Stichprobe X
n	Stichprobenumfang von Stichprobe Y
t_x	Beobachtungsumfang von Stichprobe X
t_y	Beobachtungsumfang von Stichprobe Y

Hypothesentest für eine Differenz der Mittelwerte für die Methode der Normal-Approximation

Formel

Der Test mit einer Normal-Approximation basiert auf der folgenden z-Statistik, die gemäß der Nullhypothese annähernd eine Standardnormalverteilung aufweist:

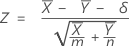
Minitab verwendet die folgenden Gleichungen für den p-Wert der jeweiligen Alternativhypothesen:

Notation

Begriff	Beschreibung
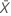	beobachteter Wert der mittleren Anzahl von Ereignissen in Stichprobe X
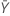	beobachteter Wert der mittleren Anzahl von Ereignissen in Stichprobe Y
δ	wahrer Wert der Differenz zwischen den Mittelwerten der Grundgesamtheit von zwei Stichproben
δ ₀	Hypothesenwert der Differenz zwischen den Mittelwerten der Grundgesamtheit von zwei Stichproben
m	Stichprobenumfang der Stichprobe X
n	Stichprobenumfang der Stichprobe Y

Hypothesentest für eine Differenz der Mittelwerte für die exakte Methode

Formel

Wenn die hypothetische Differenz gleich 0 ist, verwendet Minitab ein exaktes Verfahren. Das exakte Verfahren verwendet die folgende Nullhypothese:

Das exakte Verfahren basiert auf der folgenden Tatsache unter der Annahme, dass die Nullhypothese wahr ist:

S | W ~ Binomial(w, p)

Dabei gilt Folgendes:

W = S + U

Minitab verwendet die folgenden Gleichungen für den p-Wert der jeweiligen Alternativhypothesen:

H₁: δ > 0: p-Wert = P(S ≥ s | w = s + u, δ = 0)

H₁: δ < 0: p-Wert = P(S ≤ s | w = s + u, δ = 0)

H₁: δ ≠ 0:

wenn P(S ≤ s|w = s + u, δ = 0) ≤ 0,5

oder P(S ≥ s|w = s + u, δ = 0) ≤ 0,5

dann:
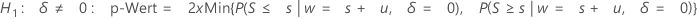
andernfalls ist der p-Wert = 1,0.

Ein beidseitiger Test ist kein gleichseitiger Test, es sei denn m = n.

Notation

Begriff	Beschreibung
μ_x	wahrer Wert der mittleren Ereignishäufigkeit in der Grundgesamtheit X
μ_y	wahrer Wert der mittleren Ereignishäufigkeit in der Grundgesamtheit Y
δ	wahrer Wert der Differenz zwischen den Mittelwerten der Grundgesamtheiten von zwei Stichproben
m	Stichprobenumfang von Stichprobe X
n	Stichprobenumfang von Stichprobe Y

Hypothesentest für eine Differenz der Mittelwerte für die Methode der zusammengefassten Mittelwerte

Formel

Wenn Sie eine Differenz von null mit der folgenden Nullhypothese testen, können Sie eine zusammengefasste Rate für beide Stichproben verwenden:

Das Verfahren der zusammengefassten Mittelwerte basiert auf dem folgenden z-Wert, der gemäß der folgenden Nullhypothese annähernd eine Standardnormalverteilung aufweist:

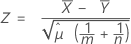
Dabei gilt Folgendes:

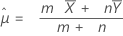
Minitab verwendet die folgenden Gleichungen für den p-Wert der jeweiligen Alternativhypothesen:

Notation

Begriff	Beschreibung
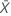	beobachteter Wert der mittleren Anzahl von Ereignissen in Stichprobe X
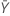	beobachteter Wert der mittleren Anzahl von Ereignissen in Stichprobe Y
µ_x	wahrer Wert der mittleren Ereignishäufigkeit in der Grundgesamtheit X
µ_y	wahrer Wert der mittleren Ereignishäufigkeit in der Grundgesamtheit Y
δ	wahrer Wert der Differenz zwischen den Mittelwerten der Grundgesamtheiten von zwei Stichproben
m	Stichprobenumfang von Stichprobe X
n	Stichprobenumfang von Stichprobe Y

Konfidenzintervall für die Differenz der Raten

Formel

Ein 100(1 – α)%-Konfidenzintervall für die Differenz zwischen zwei Poisson-Raten der Grundgesamtheiten wird wie folgt angegeben:

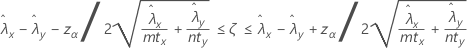
Notation

Begriff	Beschreibung
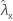	beobachteter Wert der Rate für Stichprobe X
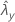	beobachteter Wert der Rate für Stichprobe Y
ζ	wahrer Wert der Differenz zwischen den Raten der Grundgesamtheiten von zwei Stichproben
z_x	Punkt des oberen x. Perzentils für die Standardnormalverteilung, wobei 0 < x < 1
m	Stichprobenumfang von Stichprobe X
n	Stichprobenumfang von Stichprobe Y
t_x	Beobachtungsumfang von Stichprobe X
t_y	Beobachtungsumfang von Stichprobe Y

Konfidenzgrenzen für die Differenz der Raten

Formel

Wenn Sie einen „Größer als“-Test angeben, wird eine untere 100(1 – α)%-Konfidenzgrenze für die Differenz zwischen zwei Ereignisraten in Poisson-Modellen der Grundgesamtheiten wie folgt angegeben:

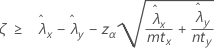
Wenn Sie einen „Kleiner als“-Test angeben, wird eine obere 100(1 – α)%-Konfidenzgrenze für die Differenz zwischen zwei Ereignisraten in Poisson-Modellen der Grundgesamtheiten wie folgt angegeben:

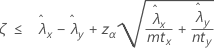
Notation

Begriff	Beschreibung
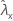	beobachteter Wert der Rate für Stichprobe X
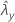	beobachteter Wert der Rate für Stichprobe Y
ζ	wahrer Wert der Differenz zwischen den Raten der Grundgesamtheiten von zwei Stichproben
z_x	Punkt des oberen x. Perzentils für die Standardnormalverteilung, wobei 0 < x < 1
m	Stichprobenumfang von Stichprobe X
n	Stichprobenumfang von Stichprobe Y
t_x	Beobachtungsumfang von Stichprobe X
t_y	Beobachtungsumfang von Stichprobe Y

Konfidenzintervall für die Differenz der Mittelwerte

Formel

Ein 100(1 – α)%-Konfidenzintervall für die Differenz zwischen zwei Poisson-Mittelwerten der Grundgesamtheit wird wie folgt angegeben:

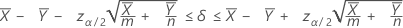
Notation

Begriff	Beschreibung
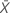	beobachteter Wert der mittleren Anzahl von Ereignissen in Stichprobe X
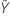	beobachteter Wert der mittleren Anzahl von Ereignissen in Stichprobe Y
δ	wahrer Wert der Differenz zwischen den Mittelwerten der Grundgesamtheit von zwei Stichproben
z_x	Punkt des oberen x. Perzentils für die Standardnormalverteilung, wobei 0 < x < 1
m	Stichprobenumfang der Stichprobe X
n	Stichprobenumfang der Stichprobe Y

Konfidenzgrenzen für die Differenz der Mittelwerte

Formel

Wenn Sie einen „Größer als“-Test angeben, wird eine untere 100(1 – α)%-Konfidenzgrenze für die Differenz zwischen zwei Poisson-Mittelwerten der Grundgesamtheiten wie folgt angegeben:

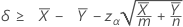
Wenn Sie einen „Kleiner als“-Test angeben, wird eine obere 100(1 – α)%-Konfidenzgrenze für die Differenz zwischen zwei Poisson-Mittelwerten der Grundgesamtheiten wie folgt angegeben:

Notation

Begriff	Beschreibung
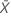	beobachteter Wert der mittleren Anzahl von Ereignissen in Stichprobe X
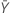	beobachteter Wert der mittleren Anzahl von Ereignissen in Stichprobe Y
δ	wahrer Wert der Differenz zwischen den Mittelwerten der Grundgesamtheiten von zwei Stichproben
z_x	Punkt des oberen x. Perzentils für die Standardnormalverteilung, wobei 0 < x < 1
m	Stichprobenumfang von Stichprobe X
n	Stichprobenumfang von Stichprobe Y