Wählen Sie die gewünschte Methode oder Formel aus.
Konfidenzintervall (KI)
Formel
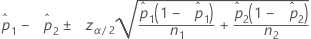
Notation
| Begriff | Beschreibung |
|---|---|
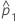 | Schätzwert des Anteils der ersten Grundgesamtheit |
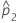 | Schätzwert des Anteils der zweiten Grundgesamtheit |
| n1 | Anzahl der Versuche in der ersten Stichprobe |
| n2 | Anzahl der Versuche in der zweiten Stichprobe |
| zα/2 | inverse kumulative Wahrscheinlichkeit der Standardnormalverteilung bei 1 – α/2 |
| α | 1 – Konfidenzniveau/100 |
Test mit Normal-Approximation
Die Berechnung der Teststatistik Z hängt von der Methode zum Schätzen von p ab.
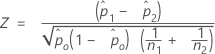
- Separate Schätzwerte von p
- In der Standardeinstellung verwendet Minitab separate Schätzwerte von p für jede Grundgesamtheit und berechnet Z wie folgt:
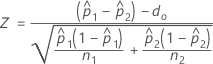
- Zusammengefasster Schätzwert von p
- Wenn die hypothetische Differenz des Tests null ist und Sie einen zusammengefassten Schätzwert von p für den Test verwenden, berechnet Minitab Z wie folgt:
Der p-Wert für jede Alternativhypothese lautet:
- H1: p1 > p2 : p-Wert = P(Z1 ≥ z)
- H1: p1 < p2 : p-Wert = P(Z1 ≤ z)
- H1: p1 ≠ p2 : p-Wert = 2P(Z1 ≥ z)
Diese Wahrscheinlichkeiten werden anhand der Standardnormalverteilung berechnet.
Notation
| Begriff | Beschreibung |
|---|---|
| p1 | tatsächlicher Anteil der Ereignisse in der ersten Grundgesamtheit |
| p2 | tatsächlicher Anteil der Ereignisse in der zweiten Grundgesamtheit |
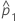 | beobachteter Anteil der Ereignisse in der ersten Stichprobe |
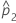 | beobachteter Anteil der Ereignisse in der zweiten Stichprobe |
| n1 | Anzahl der Versuche in der ersten Stichprobe |
| n2 | Anzahl der Versuche in der zweiten Stichprobe |
| d0 | Hypothesendifferenz zwischen dem ersten und dem zweiten Anteil |
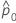 | 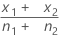 |
| x1 | Anzahl der Ereignisse in der ersten Stichprobe |
| x2 | Anzahl der Ereignisse in der zweiten Stichprobe |
Fishers exakter Test
Minitab führt neben einem Test auf der Grundlage einer Normal-Approximation Fishers exakten Test durch. Fishers exakter Test ist für alle Stichprobenumfänge gültig.
Formel
Unter der Nullhypothese weist die Anzahl der Ereignisse in der ersten Stichprobe (x1) eine hypergeometrische Verteilung mit diesen Parametern auf:
- Größe der Grundgesamtheit = n1 + n2
- Anzahl der Ereignisse in Grundgesamtheit = x1 + x2
- Stichprobenumfang = n1
Seien f( ) und F( ) die Dichtefunktion (PDF) und die kumulative Verteilungsfunktion (CDF) dieser hypergeometrischen Verteilung. Mit „Modalwert“ wird ihr Modalwert angegeben. Die p-Werte für die jeweilige Alternativhypothese lauten wie folgt:
- H1: p1 < p2
p-Wert = F(x1)
- H1: p1 > p2
p-Wert = 1 – F(x1 – 1)
- H1: p1 ≠ p2
Es gibt drei Fälle:
- Fall 1: x1 < Modalwert
p-Wert = unterer p-Wert + oberer p-Wert
Begriff Beschreibung unterer p-Wert F(x1) oberer p-Wert 1 – F(y – 1) y kleinste ganze Zahl > Modalwert, so dass f(y) <f(x1) Hinweis
Der obere p-Wert kann gleich null sein.
- Fall 2: x1 = Modalwert
p-Wert = 1,0
- Fall 3: x1 > Modalwert
p-Wert = unterer p-Wert + oberer p-Wert
Begriff Beschreibung oberer p-Wert 1 – F(x1 – 1) unterer p-Wert F(y) y größte ganze Zahl < Modalwert, so dass f(y) < f(x1) Hinweis
Der untere p-Wert kann gleich null sein.
- Fall 1: x1 < Modalwert
Notation
| Begriff | Beschreibung |
|---|---|
| p1 | tatsächlicher Anteil der Ereignisse in der ersten Grundgesamtheit |
| p2 | tatsächlicher Anteil der Ereignisse in der zweiten Grundgesamtheit |
| x1 | Anzahl der Ereignisse in der ersten Stichprobe |
| x2 | Anzahl der Ereignisse in der zweiten Stichprobe |
| n1 | Anzahl der Versuche in der ersten Stichprobe |
| n2 | Anzahl der Versuche in der zweiten Stichprobe |
