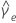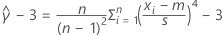In diesem Thema
Standardabweichung (StdAbw)
Die Standardabweichung ist das am häufigsten verwendete Maß für die Streuung bzw. die Streubreite der Daten um den Mittelwert. Die Standardabweichung der Stichprobe ist gleich der Quadratwurzel der Varianz der Stichprobe.
 , dann wird die Standardabweichung angegeben durch:
, dann wird die Standardabweichung angegeben durch:

Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung in der Stichprobe |
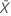 | Mittelwert der Stichprobe |
| S | Standardabweichung der Stichprobe |
| n | Stichprobenumfang |
Varianz
Die Varianz ist ein Maß der Streuung der Daten um ihren Mittelpunkt. Die Varianz ist gleich dem Quadrat der Standardabweichung.
Formel
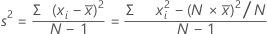
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
Konfidenzintervalle und -grenzen für die Chi-Quadrat-Methode
Konfidenzintervalle
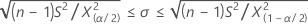

Konfidenzgrenzen
Wenn Sie einen einseitigen Test angeben, berechnet Minitab eine einseitige 100(1–α)%-Konfidenzgrenze gemäß der Richtung der Alternativhypothese.
- Wenn Sie eine „Größer als“-Alternativhypothese angeben, wird eine untere 100(1–α)%-Grenze für die Standardabweichung der Grundgesamtheit wie folgt angegeben:

Eine untere 100(1–α)%-Grenze für die Varianz der Grundgesamtheit wird wie folgt angegeben:
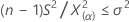
- Wenn Sie eine „Kleiner als“-Alternativhypothese angeben, wird eine obere 100(1–α)%-Grenze für die Standardabweichung der Grundgesamtheit wie folgt angegeben:

Eine obere 100(1–α)%-Grenze für die Varianz der Grundgesamtheit wird wie folgt angegeben:

Notation
| Begriff | Beschreibung |
|---|---|
| α | Alpha-Niveau für das 100(1 – α)%-Konfidenzintervall |
| n | Stichprobenumfang |
| S2 | Stichprobenvarianz |
| Χ2(p) | oberer 100p-ter Perzentilpunkt in einer Chi-Quadrat-Verteilung mit (n – 1) Freiheitsgraden |
| σ | wahrer Wert der Standardabweichung der Grundgesamtheit |
| σ2 | wahrer Wert der Varianz der Grundgesamtheit |
Konfidenzintervalle und -grenzen für die Bonett-Methode
Verwenden Sie diese Methode für alle stetigen Daten (normalverteilt oder nicht normalverteilt). 1
Konfidenzintervall

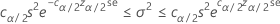
Konfidenzgrenzen
Wenn Sie einen einseitigen Test angeben, berechnet Minitab eine einseitige 100(1–α)%-Konfidenzgrenze gemäß der Richtung der Alternativhypothese.
-
Wenn Sie eine „Größer als“-Alternativhypothese angeben, wird eine untere 100(1–α)%-Grenze für die Standardabweichung der Grundgesamtheit wie folgt angegeben:
 Eine ungefähre untere 100(1- a)%-Grenze für die Varianz der Grundgesamtheit wird wie folgt angegeben:
Eine ungefähre untere 100(1- a)%-Grenze für die Varianz der Grundgesamtheit wird wie folgt angegeben:
-
Wenn Sie eine „Kleiner als“-Alternativhypothese angeben, wird eine ungefähre obere 100(1 – α)%-Grenze für die Standardabweichung der Grundgesamtheit wie folgt angegeben:
 Eine ungefähre obere 100(1 – α)%-Grenze für die Varianz der Grundgesamtheit wird angegeben durch:
Eine ungefähre obere 100(1 – α)%-Grenze für die Varianz der Grundgesamtheit wird angegeben durch: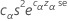
Notation
| Begriff | Beschreibung |
|---|---|
| α | 1 – Konfidenzniveau/100 |
| cα/2 | n / (n – zα/2) |
| cα | n / (n – zα ) |
| s2 | beobachteter Wert der Varianz der Stichprobe |
| zα/2 | inverse kumulative Wahrscheinlichkeit der Standardnormalverteilung bei 1 – α/2. Wenn n kleiner oder gleich zα/2 ist, berechnet Minitab keine Bonett-Konfidenzintervalle. |
| zα | inverse kumulative Wahrscheinlichkeit der Standardnormalverteilung bei 1 – α. Wenn n kleiner oder gleich zα ist, berechnet Minitab keine Bonett-Konfidenzintervalle. |
| se |  |
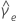 | 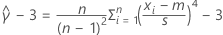 = geschätzter Kurtosis-Überschuss = geschätzter Kurtosis-Überschuss |
| m | getrimmtes Mittel mit einem Trim-Anteil gleich  ; m = Mittelwert der Stichprobe, wenn n kleiner oder gleich 5 ist ; m = Mittelwert der Stichprobe, wenn n kleiner oder gleich 5 ist |
| σ | wahrer Wert der Standardabweichung der Grundgesamtheit |
| σ2 | wahrer Wert der Varianz der Grundgesamtheit |
Hypothesentest für die Chi-Quadrat-Methode
Formel
Der Hypothesentest verwendet die folgenden Gleichungen für den p-Wert der jeweiligen Alternativhypothesen:
H1: σ2 > σ02: p-Wert = P(Χ2 ≥ x2)
H1: σ2 < σ02: p-Wert = P(Χ2 ≤ x2)
H1: σ2 ≠ σ02: p-Wert = 2 × Min{P(Χ2 ≤ x2), P(Χ2 ≥ x2)}
Notation
| Begriff | Beschreibung | ||||||
|---|---|---|---|---|---|---|---|
| σ2 | wahrer Wert der Varianz der Grundgesamtheit | ||||||
| σ02 | Hypothesenwert der Varianz der Grundgesamtheit | ||||||
| Χ2 | folgt einer Chi-Quadrat-Verteilung mit (n – 1) Freiheitsgraden, wenn σ2 = σ02 | ||||||
| x2 | 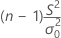
|
Hypothesentest für die Bonett-Methode
Formel
Das Bonett-Verfahren ist keiner Teststatistik zugeordnet. Minitab verwendet jedoch die Ablehnungsbereiche, die durch die Konfidenzgrenzen definiert sind, um einen p-Wert zu berechnen.
Für eine beidseitige Hypothese wird der p-Wert wie folgt angegeben:
p = 2 × Min(αU, αO)
- Für eine einseitige „Kleiner als“-Alternativhypothese wird der p-Wert als αO berechnet, nachdem α/2 in der Notation durch α ersetzt wurde.
- Für die einseitige „Größer als“-Alternativhypothese wird der p-Wert als αU berechnet, nachdem α/2 in der Notation durch α ersetzt wurde.
Notation
| Begriff | Beschreibung | ||||||
|---|---|---|---|---|---|---|---|
| σ02 | hypothetische Varianz | ||||||
| αU | kleinste Lösung α der Gleichung
 | ||||||
| αO | kleinste Lösung α der Gleichung
 | ||||||
| cα/2 | n / (n – zα/2) | ||||||
| α | 1 - Konfidenzniveau/100 | ||||||
| s2 | beobachteter Wert der Varianz der Stichprobe | ||||||
| zα/2 | inverse kumulative Wahrscheinlichkeit der Standardnormalverteilung bei 1 – α/2. Wenn n kleiner oder gleich zα/2 ist, berechnet Minitab keine Bonett-Konfidenzintervalle. | ||||||
| se | 
|