Methoden und Formeln für Ereignisrate in Poisson-Modellen, 1 Stichprobe

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Statistik
p-Wert für den exakten Test
Konfidenzintervalle und -grenzen für den exakten Test
p-Wert für die Normal-Approximation
Konfidenzintervalle und -grenzen für die Normal-Approximation

Statistik

Minitab generiert die folgende deskriptive Statistik aus Ihrer Stichprobe. Minitab zeigt nur dann einen Mittelwert an, wenn Sie den „Beobachtungsumfang“ vom Standardwert 1 in einen anderen Wert ändern.

Begriff	Beschreibung
Ereignisrate
Mittleres Vorkommen

Die Rate ist gleich der durchschnittlichen Anzahl der Vorkommen pro Einheit des Beobachtungsumfangs. Der Mittelwert ist die durchschnittliche Anzahl der Vorkommen in der gesamten Stichprobe. Wenn der Beobachtungsumfang gleich 1 ist, dann sind die Rate und der Mittelwert gleich.

p-Wert für den exakten Test

Formel

Im exakten Test für Ereignisrate in Poisson-Modellen, 1 Stichprobe werden die folgenden Gleichungen verwendet, um die p-Werte für die jeweiligen Alternativhypothesen zu berechnen:

H₁: λ > λ₀: p-Wert = P(S ≥ s | λ = λ₀), wobei S eine Poisson-Verteilung mit dem Mittelwert nλ₀t aufweist.
H₁: λ < λ₀: p-Wert = P(S ≤ s | λ = λ₀), wobei S eine Poisson-Verteilung mit dem Mittelwert nλ₀t aufweist.
H₁: λ ≠ λ₀: Minitab verwendet einen Likelihood-Quotienten-Test wie folgt:
Sei G(s) die Funktion, die den Likelihood-Quotienten-Test in Bezug auf s ausdrückt, der Gesamt-Ereignishäufigkeit im Poisson-Prozess:
- Wenn 0 ≤ s < nλ₀t, wird die Gleichung G(y) = G(s) für y im Intervall (nλ₀t, enλ₀t] gelöst;
  p-Wert = P(S ≤ s | λ = λ₀) + P(S ≥ y | λ = λ₀)
- Wenn s = nλ₀t, dann
  p-Wert = 1,00
- Wenn nλ₀t < s ≤ enλ₀t, wird die Gleichung G(y) = G(s) für y im Intervall [0, nλ₀t) gelöst;
  p-Wert = P(S ≤ y | λ = λ₀) + P(S ≥ s | λ = λ₀)
- Wenn s > enλ₀t, ist der Test einseitig und
  p-Wert = P(S ≥ s | λ = λ₀)
wobei S eine Poisson-Verteilung mit dem Mittelwert nλ₀t aufweist.

Notation

Begriff	Beschreibung
s	Gesamt-Ereignishäufigkeit im Poisson-Prozess
t	Beobachtungsumfang
λ₀	hypothetischer Wert des Parameters für die Rate der Grundgesamtheit
λ	wahrer Wert des Parameters für die Rate der Grundgesamtheit
n	Stichprobenumfang
e	2,71828 (ungefährer Wert)

Konfidenzintervalle und -grenzen für den exakten Test

Konfidenzintervalle

Ein exaktes 100(1 – α)%-Konfidenzintervall für die Ereignisrate eines Poisson-Prozesses wird wie folgt angegeben:

Wenn Sie einen Wert des „Beobachtungsumfangs“ angeben, zeigt Minitab auch ein Konfidenzintervall für die mittlere Ereignishäufigkeit an. Dieses Konfidenzintervall wird wie folgt angegeben:

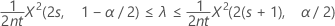
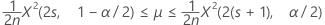
Konfidenzgrenzen

Wenn Sie einen einseitigen Test angeben, berechnet Minitab eine einseitige 100(1 – α)%-Konfidenzgrenze gemäß der Richtung der Alternativhypothese.

Wenn Sie eine „Größer als“-Alternativhypothese angeben, wird die exakte untere 100(1 – α)%-Grenze der Rate wie folgt angegeben:

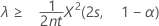
Die exakte untere 100(1 – α)%-Grenze des Mittelwerts wird wie folgt angegeben:
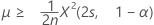
Wenn Sie eine „Kleiner als“-Alternativhypothese angeben, wird die exakte obere 100(1 – α)%-Grenze der Rate wie folgt angegeben:

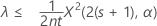
Die exakte obere 100(1 – α)%-Grenze des Mittelwerts wird wie folgt angegeben:

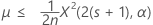
Notation

Begriff	Beschreibung
s	Gesamt-Ereignishäufigkeit im Poisson-Prozess
t	Beobachtungsumfang
λ	wahrer Wert der Rate der Grundgesamtheit
μ	wahrer Wert des Mittelwerts der Grundgesamtheit
Χ²_{(p, x)}	oberer x-ter Perzentilpunkt der Χ²-Verteilung mit p Freiheitsgraden, wobei 0 < x < 1.
α	Alpha-Niveau für das 100(1–α)%-Konfidenzintervall
n	Stichprobenumfang

p-Wert für die Normal-Approximation

Normal-Approximationen sind gültig, wenn die Gesamtzahl der Ereignisse größer als 10 ist.

Formel

Der auf einer Normal-Approximation basierende Hypothesentest für Ereignisrate in Poisson-Modellen, 1 Stichprobe verwendet die folgenden Gleichungen für den p-Wert der jeweiligen Alternativhypothesen:

Notation

Begriff	Beschreibung
Z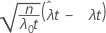
t	Beobachtungsumfang
λ ₀	Hypothesenwert des Parameters für die Ereignisrate der Grundgesamtheit
λ	wahrer Wert des Parameters für die Ereignisrate der Grundgesamtheit
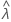	beobachteter Wert der Ratenstatistik der Stichprobe
n	Stichprobenumfang

Konfidenzintervalle und -grenzen für die Normal-Approximation

Konfidenzintervalle

Ein 100(1 – α)%-Konfidenzintervall auf der Grundlage einer Normal-Approximation für die Ereignisrate eines Poisson-Prozesses wird wie folgt angegeben:

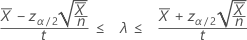
Wenn Sie einen Wert des „Beobachtungsumfangs“ angeben, zeigt Minitab auch ein Konfidenzintervall für die mittlere Ereignishäufigkeit an. Dieses Konfidenzintervall wird wie folgt angegeben:

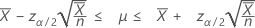
Konfidenzgrenzen

Wenn Sie einen einseitigen Test angeben, berechnet Minitab eine einseitige 100(1 – α)%-Konfidenzgrenze gemäß der Richtung der Alternativhypothese.

Wenn Sie eine „Größer als“-Alternativhypothese angeben, wird die exakte untere 100(1 – α)%-Grenze der Rate wie folgt angegeben:

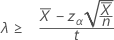
Wenn Sie einen Wert des „Beobachtungsumfangs“ angeben, wird die exakte untere 100(1-α)%-Grenze des Mittelwerts wie folgt angegeben:
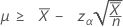
Wenn Sie eine „Kleiner als“-Alternativhypothese angeben, wird die exakte obere 100(1 – α)%-Grenze der Rate wie folgt angegeben:

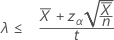
Wenn Sie einen Wert des „Beobachtungsumfangs“ angeben, wird die exakte obere 100(1-α)%-Grenze des Mittelwerts wie folgt angegeben:

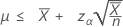
Notation

Begriff	Beschreibung
s	Gesamt-Ereignishäufigkeit im Poisson-Prozess
t	Beobachtungsumfang
λ	wahrer Wert der Rate der Grundgesamtheit
μ	wahrer Wert des Mittelwerts der Grundgesamtheit
Z_x	Punkt des oberen x. Perzentils für die Standardnormalverteilung, wobei 0 < x < 1
α	Alpha-Niveau für das 100(1–α)%-Konfidenzintervall
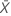	mittlere Ereignishäufigkeit in der Stichprobe
n	Stichprobenumfang