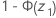In diesem Thema
- Angepasstes exaktes Blaker-Konfidenzintervall und Testmethoden
- Clopper-Pearson-Methode mit exaktem Konfidenzintervall
- Test, der dem exakten Clopper-Pearson-Konfidenzintervall entspricht
- Wilson-Score-Konfidenzintervall-Methode
- Punktetest
- Agresti-Coull-Konfidenzintervall und Testmethoden
- Konfidenzintervall für Wald-Normalapproximation (Web-App)
Angepasstes exaktes Blaker-Konfidenzintervall und Testmethoden
Die angepasste Blaker-Exact-Methode erzeugt zweiseitige Konfidenzintervalle für den Anteil der Ereignisse und erzeugt p-Werte für die Alternativhypothese von p ≠ p0. Blaker12 liefert ein exaktes, zweiseitiges Konfidenzintervall, indem die p-Wert-Funktion eines exakten Tests invertiert wird. Die Clopper-Pearson-Intervalle sind breiter und enthalten immer die Blaker-Konfidenzintervalle. Intervalle aus der Blaker-Exact-Methode sind verschachtelt. Diese Eigenschaft bedeutet, dass Konfidenzintervalle mit höheren Konfidenzniveaus Konfidenzintervalle mit niedrigeren Konfidenzniveaus enthalten. Beispielsweise enthält ein exaktes, zweiseitiges Blaker-95%-Konfidenzintervall das entsprechende 90%-Konfidenzintervall.
Die ursprüngliche exakte Methode von Blaker hat 2 Einschränkungen. Eine Einschränkung besteht darin, dass der numerische Algorithmus zur Berechnung der Konfidenzintervalle langsam ist, insbesondere wenn der Stichprobenumfang groß ist. Eine weitere Einschränkung besteht darin, dass die ursprüngliche Blaker-Exact-Methode für einige Daten ein Intervall erzeugt, das einen hypothetischen Anteil abdeckt, wenn der p-Wert kleiner als das Signifikanzniveau ist, das dem Konfidenzniveau entspricht. Die Einschränkung tritt auch auf, wenn das Konfidenzintervall keinen hypothetischen Anteil enthält, wenn der p-Wert größer als das Signifikanzniveau ist, das dem Konfidenzniveau entspricht.
Um diese Einschränkungen zu überwinden, werden bei der Analyse in der Minitab Statistical Software das Konfidenzintervall und der p-Wert mit dem Algorithmus von Klaschka und Reiczigel erstellt.3 Der Name dieser Methode ist die angepasste Blaker-Exact-Methode. Dieser numerische Algorithmus ist schneller zu berechnen und erzeugt Konfidenzintervalle und Tests, die im Allgemeinen übereinstimmen. Die angepassten Blaker-Konfidenzintervalle sind ebenfalls exakt und verschachtelt.
Für eine Alternativhypothese mit kleiner als oder mit größer als wird die Clopper-Pearson-Methode verwendet.
Clopper-Pearson-Methode mit exaktem Konfidenzintervall
Das Intervall (PL, PU) ist ein zweiseitiges Konfidenzintervall von 100(1 – α)% von p. Wenn die Stichprobe keine Ereignisse aufweist, ist die Untergrenze 0. Wenn die Stichprobe nur Ereignisse enthält, ist die Obergrenze 1.
Untergrenze
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| V1 | 2x |
| V2 | 2(n – x + 1) |
| x | Anzahl der Ereignisse |
| n | Anzahl der Versuche |
| F | unterer α/2-Punkt der F-Verteilung mit v1 - undv2-Freiheitsgraden |
Obergrenze
Formel
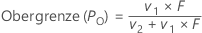
Notation
| Begriff | Beschreibung |
|---|---|
| V1 | 2(x + 1) |
| V2 | 2(n – x) |
| x | Anzahl der Ereignisse |
| n | Anzahl der Versuche |
| F | oberer α/2-Punkt der F-Verteilung mit Freiheitsgraden v1 und v2 |
Test, der dem exakten Clopper-Pearson-Konfidenzintervall entspricht
Formel
- Ha: p ≠ p0
- p-Wert =
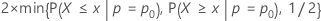
- Ha: p > p0
- p-Wert = P{ X ≥ x | p = po}
- Ha: p < p0
- p-Wert = P{ X ≤ x | p = po}
Notation
| Begriff | Beschreibung |
|---|---|
| p0 | Hypothesenanteil |
| n | Anzahl der Versuche |
| p | Ereigniswahrscheinlichkeit |
| x | Anzahl der Ereignisse |
Wilson-Score-Konfidenzintervall-Methode
Wilson4 invertiert den Score-Test, um Konfidenzintervalle zu erhalten, die von der Minitab Statistical Software als Wilson-Score-Konfidenzintervalle bezeichnet werden. Wilson-Score-Intervalle haben zwei Formen, eine ohne Kontinuitätskorrektur und eine mit einer Kontinuitätskorrektur. Die Abdeckung der Intervalle ohne die Korrektur liegt manchmal unter dem nominalen Konfidenzniveau. Das tatsächliche Konfidenzniveau der Intervalle mit der Korrektur ist mindestens das nominale Konfidenzniveau. Bei beiden Methoden, bei denen die Stichprobe keine Ereignisse aufweist, liegt die Untergrenze bei 0. Wenn die Stichprobe nur Ereignisse enthält, ist die Obergrenze 1.
Intervalle ohne Durchgangskorrektur
Das zweiseitige Konfidenzintervall von 100(1 – α)% hat die folgende Formel:
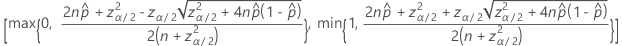
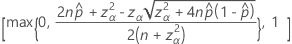
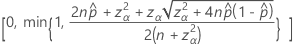
Intervalle mit der Durchgangskorrektur
Die Untergrenze des zweiseitigen Intervalls 100(1 – α)% hat die folgende Formel:
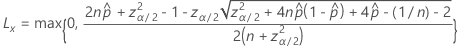
Die obere Grenze des zweiseitigen Intervalls 100(1 – α)% hat die folgende Formel:
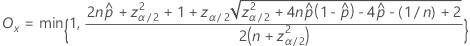
Die einseitige Untergrenze von 100 (1 – α) % hat folgende Formel:
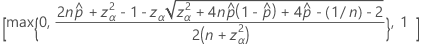
Die einseitige Obergrenze von 100 (1 – α) % hat folgende Formel:
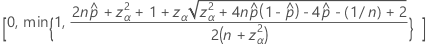
Notation
| Begriff | Beschreibung |
|---|---|
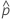 | beobachtete Wahrscheinlichkeit, 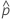 = x / n = x / n |
| x | Anzahl der Ereignisse |
| n | Anzahl der Versuche |
| zγ | Der obere Perzentilpunkt der Standardnormalverteilung bei γ |
| α | 1 – Konfidenzniveau/100 |
Punktetest
Methode ohne Kontinuitätskorrektur
Der Test, der dem Wilson-Score-Konfidenzintervall und der normalen Approximationsmethode (Web-App) entspricht, ist der bekannte Score-Test. Die Ergebnisteststatistik hat die folgende Gleichung:
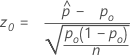
- Ha: p ≠ p0
- p-Wert =
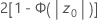
- Ha: p > p0
- p-Wert =

- Ha: p < p0
- p-Wert =

Methode mit der Kontinuitätskorrektur
Die Teststatistik und der p-Wert für das Verfahren mit Kontinuitätskorrektur hängen von der Alternativhypothese ab.
- Ha: p ≠ p0
-
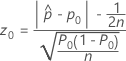
- Ha: p > p0
-
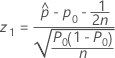
- Ha: p < p0
-
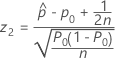
Notation
| Begriff | Beschreibung |
|---|---|
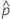 | beobachtete Wahrscheinlichkeit, x/n |
| x | Anzahl der Ereignisse |
| n | Anzahl der Versuche |
| p0 | Hypothesenanteil |
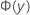 | Kumulative Verteilungsfunktion der Standardnormalverteilung bei y |
Agresti-Coull-Konfidenzintervall und Testmethoden
Konfidenzintervall
Agresti und Coull5 bieten eine Anpassung der Wald-Methode für Konfidenzintervalle, die die Deckungseigenschaften verbessert. Bei einem zweiseitigen Konfidenzintervall von 95 % addiert die Anpassung ungefähr 2 Ereignisse und 2 Nicht-Ereignisse und berechnet dann die Konfidenzintervalle aus den Formeln für die Wald-Konfidenzintervallformeln. Wenn die Stichprobe keine Ereignisse aufweist, ist die Untergrenze 0. Wenn die Stichprobe nur Ereignisse enthält, ist die Obergrenze 1.
Das zweiseitige Intervall 100(1 – α)% hat die folgende Formel:
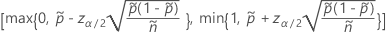
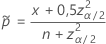
und
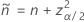
Die einseitige Untergrenze von 100 (1 – α) % hat folgende Formel:
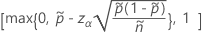
Die einseitige Obergrenze von 100 (1 – α) % hat folgende Formel:
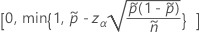
Für die einseitigen Grenzwerte verwenden Sie  bei der Definition von
bei der Definition von 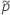 und
und 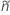 :
:
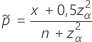
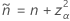
Test, der dem Agresti-Coull-Intervall entspricht
Bei der Analyse wird der p-Wert für den Test berechnet, indem das Konfidenzintervallverfahren invertiert wird.
Notation
| Begriff | Beschreibung |
|---|---|
| x | Anzahl der Ereignisse |
| n | Anzahl der Versuche |
| zγ | Der obere Perzentilpunkt der Standardnormalverteilung bei γ |
| α | 1 – Konfidenzniveau/100 |
Konfidenzintervall für Wald-Normalapproximation (Web-App)
Formel
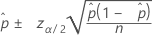
Notation
| Begriff | Beschreibung |
|---|---|
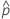 | beobachtete Wahrscheinlichkeit, 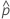 = x / n = x / n |
| x | beobachtete Anzahl von Ereignissen in n Versuchen |
| n | Anzahl der Versuche |
| zα/2 | inverse kumulative Wahrscheinlichkeit der Standardnormalverteilung bei 1–α/2 |
| α | 1 – Konfidenzniveau/100 |