In diesem Thema
Optimierungsdiagramm
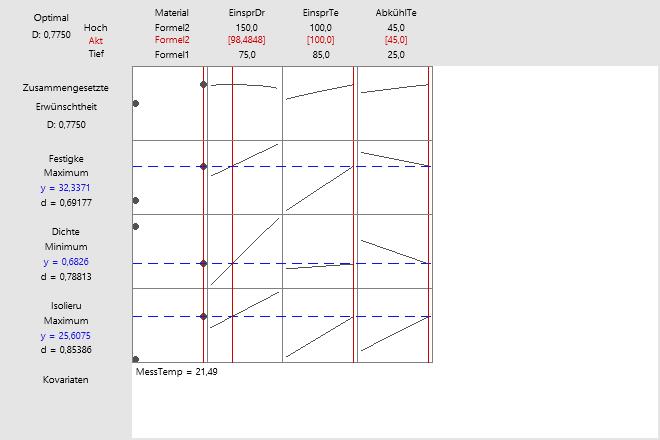
Das Optimierungsdiagramm zeigt, wie sich die Variablen auf die vorhergesagten Antworten auswirken. Wenn das Optimierungsdiagramm interaktiv ist, zeigen die Zellen, wie sich die entsprechende Antwortvariable oder die zusammengesetzte Erwünschtheit in Abhängigkeit von einer der Variablen ändert, während alle anderen Variablen unverändert bleiben. Das Optimierungsdiagramm stellt die angepassten Werte für die Prädiktoreinstellungen dar.
- Spalte für jede Variable (Prädiktor)
- Die vertikalen roten Linien in der Grafik geben die aktuellen Einstellungen an.
- Zeilen für jede Antwortvariable.
- Die horizontalen blauen Linien stellen die aktuellen Werte der Antwortvariablen dar.
- Zusammengesetzte Erwünschtheit
- In der oberen Reihe und in der oberen linken Ecke befindet sich die zusammengesetzte Erwünschtheit (D).
- Interaktive Symbolleiste
- Mit der Schaltfläche „Prognostizieren“ oben links auf der Symbolleiste wird die Prognose für die aktuellen Variableneinstellungen berechnet.
Der von Minitab angezeigte Typ der angepassten Werte hängt von dem Typ der Antwortvariablen in Ihrem Modell ab. Minitab zeigt z. B. Mittelwerte, Wahrscheinlichkeiten oder Standardabweichungen an, je nachdem, ob Sie über kontinuierliche oder Zählmessungen, Binärdaten oder Modelle verfügen, die Streuung analysieren.
- Statistik
- Doppelklicken Sie auf das Optimierungsdiagramm, um es interaktiv zu machen.
- Predictive Analytics-Modul
- Die Handlung ist immer interaktiv.
Interpretation
Verwenden Sie das Optimierungsdiagramm, um die optimalen Einstellungen für die Prädiktoren bei den von Ihnen angegebenen Parametern zu ermitteln.
- Material: Die zwei Punkte für jede Zelle in dieser Spalte stellen die beiden Ebenen der kategorialen Variablen dar: Formula1 und Formula2. „Formel2“ ist anscheinend das beste Material. Durch einen Wechsel zu „Formel1“ würde der Dämmwert sinken und die Dichte zunehmen. Dies ist beides unerwünscht. Da der Materialtyp jedoch mit anderen Faktoren interagiert, gilt dieser Trend möglicherweise nicht für andere Einstellungen. Überlegen Sie, ob Sie eine lokale Lösung für die Formel 1 finden können. Oder ändern Sie die Einstellungen für Formel1 direkt im Diagramm, indem Sie die vertikalen Balken verschieben.
- EinsprDruck: Durch das Erhöhen des Einspritzdrucks werden die Werte aller drei Antwortvariablen erhöht. Daher liegt die optimale Einstellung in der Mitte des Bereichs (98,4848), was einen Kompromiss zwischen widersprüchlichen Zielen darstellt. Ziel ist es, den Isolationswert zu maximieren, die Dichte zu minimieren und die Festigkeit zu maximieren.
- EinsprTemp: Eine Erhöhung der Einspritztemperatur erhöht auch alle Ansprechwirkungen. Aber der Einfluss auf die Dichte ist minimal im Vergleich zu dem Effekt auf den Dämmwert. Die zusammengesetzte Erwünschtheit wird also gesteigert, wenn die Einspritztemperatur maximiert wird. Die optimalen Einstellungen der Einspritztemperatur liegen bei den maximalen Werten im Versuch. Dieses Ergebnis verweist darauf, dass Sie mit höheren Temperaturen experimentieren sollten.
- AbkühlTemp: Das Erhöhen der Abkühltemperatur erhöht den Dämmwert, allerdings nehmen Dichte und Festigkeit ab. Die optimalen Einstellungen sowohl der Einspritztemperatur als auch der Kühltemperatur liegen auf den maximalen Werten des Experiments. Dieses Ergebnis verweist darauf, dass Sie mit höheren Temperaturen experimentieren sollten. Sie können an den Diagrammen erkennen, dass höhere Abkühltemperaturen möglicherweise die Ergebnisse optimieren könnten. Wenn die Diagramme extrapoliert werden könnten, würden höhere Abkühltemperaturen den Dämmwert und die Dichte verbessern. Die Festigkeit würde jedoch abnehmen.
Untersuchen Sie bei einem linearen Regressionsmodell Vorhersageintervalle, um zu bestimmen, ob der Bereich der wahrscheinlichen Werte für einen einzelnen zukünftigen Wert innerhalb akzeptabler Grenzen für den Prozess liegt. Graue Bereiche zeigen an, wo der entsprechende Wert der Antwortvariablen eine Erwünschtheit von null aufweist.
Parameter
Minitab zeigt die Versuchsplanparameter für jede Antwortvariablen in der Tabelle Parameter an. Untersuchen Sie diese Ergebnisse, um sicherzustellen, dass die angezeigten Konstruktionsparameter korrekt sind.
Ihre Auswahl von Ziel, Unterzahl, Ziel, Obergrenze und Gewichtung definiert die Erwünschtheitsfunktion für jede einzelne Antwort. Die Wichtigkeitsparameter bestimmen, wie die Erwünschtheitsfunktionen zu einer einzigen zusammengesetzten Erwünschtheit kombiniert werden.
- Das Zielgrößenoptimierung Menü Statistik enthält die Optimierung für mehrere Antworten.
- Das Zielgrößenoptimierung auf der Predictive Analytics-Modul beinhaltet Optimierung für eine einzelne Antwort.
- Welche Zielsetzung in der Zielgrößenoptimierung sollte verwendet werden?
- Festlegen eines Sollwerts, einer Unter- und einer Obergrenze in der Zielgrößenoptimierung
- Ermitteln der Gewichtung in der Zielgrößenoptimierung
- Was ist unter der Bedeutung in der Zielgrößenoptimierung zu verstehen?
- Was sind die individuelle Erwünschtheit und zusammengesetzte Erwünschtheit?
Interpretation
- Das Ziel für „Festigkeit“ ist das Maximieren. Ein Wert von 38,1821 wird als sehr gut betrachtet, und Werte unter 19,2189 sind nicht akzeptabel.
- Das Ziel für „Dichte“ ist das Minimieren. Ein Wert von 0,4351 wird als sehr gut betrachtet, und Werte über 1,60314 sind nicht akzeptabel.
- Das Ziel für „Isolierung“ ist das Maximieren. Ein Wert von 27,7156 wird als sehr gut betrachtet, und Werte unter 13,2905 sind nicht akzeptabel.
Alle drei Antworten haben den gleichen Wichtigkeitswert. Daher wirken sich alle drei Antwortvariablen gleich auf die zusammengesetzte Erwünschtheit aus.
Mehrere Antwortprognosen
| Variable | Einstellung |
|---|---|
| Material | Formel2 |
| EinsprDruck | 98,4848 |
| EinsprTemp | 100 |
| AbkühlTemp | 45 |
| MessTemp | 21,4875 |
| Antwort | Anpassung | SE Anpassung | 95%-KI | 95%-PI |
|---|---|---|---|---|
| Festigkeit | 32,34 | 1,04 | (29,45; 35,22) | (27,25; 37,43) |
| Dichte | 0,6826 | 0,0597 | (0,5167; 0,8484) | (0,3899; 0,9753) |
| Isolierung | 25,608 | 0,268 | (24,863; 26,352) | (24,294; 26,921) |
Vorhersage der Antwort
Minitab verwendet die Variableneinstellungen in dieser Tabelle, um die Anpassungen für alle Antwortvariablen zu berechnen, die im Optimierungsverfahren enthalten sind.
- Das Zielgrößenoptimierung Menü Statistik enthält die Optimierung für mehrere Antworten.
- Das Zielgrößenoptimierung auf der Predictive Analytics-Modul beinhaltet Optimierung für eine einzelne Antwort.
Wenn Sie zum ersten Mal ausführen Zielgrößenoptimierung, zeigt die Vorhersagetabelle für Mehrfachantworten die optimalen Werte an, die der Algorithmus identifiziert. Wenn Sie die Variableneinstellungen im Diagramm ändern und auf die Prognose Schaltfläche in der Symbolleiste klicken, erstellt Minitab eine Tabelle mit den neuen Einstellungen.
Verwenden Sie diese Tabelle, um sich zu vergewissern, dass die Analyse wie gewünscht durchgeführt wurde.
Anpassung
Angepasste Werte sind auch bekannt als Anpassungen oder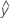 
. Die angepassten Werte sind Punktschätzungen des Mittelwerts der Antwortvariablen für die gegebenen Werte der Prädiktoren. Die Werte der Prädiktoren werden auch als x-Werte bezeichnet. Minitab verwendet die Regressionsgleichung und die Variableneinstellungen, um die Anpassung zu berechnen.
Der von Minitab angezeigte Typ der angepassten Werte hängt von dem Typ der Antwortvariablen in Ihrem Modell ab. Minitab zeigt beispielsweise Mittelwerte, Wahrscheinlichkeiten und Standardabweichungen in Abhängigkeit davon ab, ob stetige Messwerte oder Zähldaten, binäre Daten oder Modelle vorliegen, die Streuung analysieren verwenden.
Interpretation
Die angepassten Werte werden berechnet, indem x-Werte in die Modellgleichung für eine Antwortvariable eingesetzt werden.
Wenn die Gleichung beispielsweise y = 5 + 10x lautet, ergibt ein x-Wert von 2 den angepassten Wert 25 (25 = 5 + 10(2)).
SE Anpassung
Der Standardfehler der Anpassung (SE Anpassung) ist ein Schätzwert der Streuung im geschätzten Mittelwert der Antwort für die angegebenen Variableneinstellungen. Der Standardfehler der Anpassung wird bei der Berechnung des Konfidenzintervalls für den Mittelwert der Antwortvariablen verwendet. Standardfehler sind immer nicht negativ. Die Analyse berechnet Standardfehler für Modelle aus dem Statistik Menü und Modelle aus Lineare Regression und Binäre logistische Regression aus der Predictive Analytics-Modul.
Interpretation
Verwenden Sie den Standardfehler der Anpassung, um zu ermitteln, wie genau der Schätzwert für den Mittelwert der Antwort ist. Je kleiner der Standardfehler, desto genauer ist der prognostizierte Mittelwert der Antwort. Ein Analytiker entwickelt beispielsweise ein Modell, um die Lieferzeit zu prognostizieren. Für einen Satz von Variableneinstellungen prognostiziert das Modell eine mittlere Lieferzeit von 3,80 Tagen. Der Standardfehler der Anpassung für diese Einstellungen beträgt 0,08 Tage. Für einen zweiten Satz von Variableneinstellungen errechnet das Modell dieselbe mittlere Lieferzeit mit einem Standardfehler der Anpassung von 0,02 Tagen. Der Analytiker kann sich sicherer sein, dass die mittlere Lieferzeit für den zweiten Satz von Variableneinstellungen nahe an 3,80 Tagen liegt.
Mit dem angepassten Wert können Sie den Standardfehler der Anpassung verwenden, um ein Konfidenzintervall für die mittlere Antwortvariablen zu erstellen. Abhängig von der Anzahl der Freiheitsgrade erstreckt sich ein Konfidenzintervall von 95 % beispielsweise über und unter den vorhergesagten Mittelwert. Für die Lieferzeiten beträgt das 95%-Konfidenzintervall des prognostizierten Mittelwerts von 3,80 Tagen bei einem Standardfehler von 0,08 (3,64; 3,96) Tage. Sie können zu 95 % sicher sein, dass der Mittelwert der Grundgesamtheit innerhalb dieses Bereichs liegt. Wenn der Standardfehler 0,02 beträgt, ist das 95%-Konfidenzintervall (3,76; 3,84) Tage. Das Konfidenzintervall für den zweiten Satz von Variableneinstellungen ist schmaler, weil der Standardfehler kleiner ist.
95%-CI
Das Konfidenzintervall für die Anpassung gibt einen Bereich wahrscheinlicher Werte für den Mittelwert der Antwort bei bestimmten Einstellungen der Prädiktoren an. Die Analyse berechnet Konfidenzintervalle für Modelle aus dem Statistik Menü und Modelle aus Lineare Regression und Binäre logistische Regression aus dem Predictive Analytics-Modul.
Interpretation
Verwenden Sie das Konfidenzintervall, um die Schätzung des angepassten Werts für die beobachteten Werte der Variablen zu bewerten.
Bei einem Konfidenzniveau von 95 % können Sie z. B. zu 95 % sicher sein, dass das Konfidenzintervall den Mittelwert der Grundgesamtheit für die angegebenen Werte der Variablen im Modell enthält. Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihrer Ergebnisse beurteilen. Bestimmen Sie anhand Ihrer Fachkenntnisse, ob das Konfidenzintervall Werte umfasst, die in der jeweiligen Situation von praktischer Signifikanz sind. Ein breites Konfidenzintervall deutet darauf hin, dass Sie sich bezüglich des Mittelwerts von künftigen Werten weniger sicher sein können. Wenn das Intervall zu breit und damit nicht hilfreich ist, erwägen Sie, den Stichprobenumfang zu vergrößern.
95%-PI
Das Prognoseintervall ist ein Bereich, der wahrscheinlich einen einzelnen künftigen Wert der Antwortvariablen für eine ausgewählte Kombination von Variableneinstellungen enthält. Die Analyse berechnet Prognoseintervall für Modelle aus dem Statistik Menü und Modelle aus Lineare Regression Predictive Analytics-Modul dem Menü .
Interpretation
Verwenden Sie die Prognoseintervall (PI), um die Genauigkeit der Vorhersagen zu bewerten.Anhand der Prognoseintervalle können Sie die praktische Signifikanz Ihrer Ergebnisse beurteilen.Wenn ein Prognoseintervall die akzeptablen Grenzen überschreitet, sind die Prognosen für Ihre Anforderungen möglicherweise nicht genau genug.
Bei einem 95%-PI können Sie sich zu 95 % sicher sein, dass das Intervall bei den von Ihnen angegebenen Einstellungen für die Prädiktoren einen einzelnen Wert der Antwortvariablen enthält. Das Prognoseintervall ist immer breiter als das Konfidenzintervall. Dies ist auf die zusätzliche Ungewissheit beim Prognostizieren eines einzelnen Werts der Antwortvariablen gegenüber dem Mittelwert der Antwort zurückzuführen.
Ein Materialtechniker in einem Möbelwerk entwickelt beispielsweise ein einfaches Regressionsmodell, um die Steife einer Spanplatte anhand der Dichte der Platte zu prognostizieren. Der Techniker vergewissert sich, dass das Modell die Annahmen der Analyse erfüllt. Anschließend verwendet er das Modell zum Prognostizieren der Steife.
Die Regressionsgleichung prognostiziert, dass die Steife für eine neue Beobachtung mit einer Dichte von 25 gleich –21,53 + 3,541*25 oder 66,995 ist. Obwohl es unwahrscheinlich ist, dass eine solche Beobachtung eine Steife von exakt 66,995 aufweist, gibt das Prognoseintervall an, dass sich der Techniker zu 95 % sicher sein kann, dass der tatsächliche Wert ungefähr zwischen 48 und 86 liegt.
Zusammengesetzte Erwünschtheit
Verwenden Sie die zusammengesetzte Erwünschtheit (D), um zu bewerten, wie gut die Einstellungen eine Reihe von Antwortvariablen insgesamt optimieren. Die Erwünschtheit hat einen Bereich von null bis eins. Eins repräsentiert den Idealfall; null weist darauf hin, dass eine oder mehrere Antwortvariablen außerhalb ihrer akzeptablen Grenzen liegen.
- Das Zielgrößenoptimierung Menü Statistik enthält die Optimierung für mehrere Antworten.
- Das Zielgrößenoptimierung auf der Predictive Analytics-Modul beinhaltet Optimierung für eine einzelne Antwort.
Wenn mehrere Antwortvariablen vorliegen, gibt es häufig keine Faktoreinstellung, die gleichzeitig die Erwünschtheit aller Antwortvariablen maximiert. Aus diesem Grund maximiert Minitab die zusammengesetzte Erwünschtheit. Die zusammengesetzte Erwünschtheit kombiniert die individuelle Erwünschtheit aller Antwortvariablen in einem einzigen Maß. Auf die Antwortvariablen mit der größten Bedeutung wird größeres Gewicht gelegt.
Weitere Informationen finden Sie unter Was sind die individuelle Erwünschtheit und zusammengesetzte Erwünschtheit?.
Interpretation
Zusammengesetzte Erwünschtheitswerte, die nahe bei 1 liegen, geben an, dass mit den Einstellungen für alle Antwortvariablen günstige Ergebnisse erzielt werden.
