In diesem Thema
Tabelle der Gruppierungsinformationen für paarweise Mehrfachvergleiche
Minitab verwendet die Konfidenzintervalle für die Differenz zwischen zwei Stufenmittelwerten, um die Gruppierungsinformationen zu berechnen. Die Gruppierungsinformationen werden in einer Matrix angeordnet. Wenn ein Term beispielsweise k Stufen aufweist, ist die maximale Größe der Matrix k x k. Wenn sämtliche Stufen in einer Gruppe enthalten sind, ist die Größe gleich k x 1, wobei der Buchstabe „A“ für alle Faktorstufen steht. Wenn alle Stufen in verschiedenen Gruppen enthalten sind, ist die Größe gleich k x k, wobei sich Buchstaben nur auf der Diagonalen befinden.
- Alle Mittelwerte der kleinsten Quadrate auf verschiedenen Stufen eines Terms werden in absteigender Reihenfolge sortiert; dies wird angegeben als 1, 2, ... , k.
- Es wird eine k x k-Matrix mit dem Wert 0 in jeder Zelle definiert, wobei k gleich der Anzahl der Faktorstufen ist.
- Für Spalte j (wobei j = 1, ...) führt Minitab Folgendes aus:
- Die Konfidenzintervalle von Mittelwert j – Mittelwert r werden überprüft, wobei r = j + 1, ..., k. Wenn das Intervall für r den Wert 0 enthält, wird die Zelle am Schnittpunkt der r-ten Zeile und der j-ten Spalte auf 1 gesetzt.
- Die Zelle (j, j) wird auf 1 gesetzt, wenn mindestens eine Zelle in Spalte j den Wert 1 enthält.
- Die Zeilensummen von Spalte 1 bis Spalte j für Zeile I = j + 1, ... , k werden berechnet. Wenn Min(alle Zeilensummen) >= 1, wird die Schleife beendet; andernfalls wird j um 1 erhöht und das Verfahren bei Schritt a fortgesetzt.
- Für jede Zeile i prüft Minitab die Summe aller Spaltenwerte für die Zeile ≥ 1. Wenn die Summe gleich null ist, wird die Zelle am Schnittpunkt von Zeile i und Spalte j auf 1 gesetzt, wobei Spalte j die erste Spalte in der Matrix mit 0 Werten darstellt. Bei diesem Verfahren wird eine Matrix mit den Werten 1 und 0 erstellt. Die Gesamtzahl der Gruppen entspricht der Anzahl der Spalten, die ungleich null sind.
- Minitab ordnet den Spalten Buchstaben zu (z. B. A zu Spalte 1, B zu Spalte 2 usw.) und weist Zellen mit dem Wert 1 den entsprechenden Buchstaben zu.
Tabelle der Gruppierungsinformationen für Mehrfachvergleiche mit einer Kontrolle
Minitab verwendet die Ergebnisse der Konfidenzintervalle für die Differenz zwischen den einzelnen Stufenmittelwerten und der Kontrollstufe, um die Gruppierungsinformationen zu berechnen. Die Gruppierungsinformationen werden in einer Matrix mit einer Spalte abgelegt.
Minitab weist der Kontrollstufe den Buchstaben „A“ zu.
Wenn ein Intervall den Wert 0 enthält, befindet sich der Stufenmittelwert in derselben Gruppe wie die Kontrollstufe. Minitab weist dem Stufenmittelwert den Buchstaben „A“ zu.
Wenn ein Intervall den Wert null nicht enthält, wird kein Buchstabe zugewiesen.
Tukey-Methode
Formel
Die Tukey-Methode ist für alle paarweisen Vergleiche verfügbar. Die Formel für die Konfidenzintervalle lautet wie folgt:
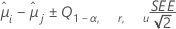
Die Formel für die Teststatistik lautet wie folgt:

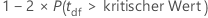
Einzelheiten zur Berechnung des korrigierten p-Werts finden Sie in den unten aufgeführten Veröffentlichungen.
Verwenden Sie die folgende Formel, um die individuelle Irrtumswahrscheinlichkeit anhand der simultanen Irrtumswahrscheinlichkeit zu ermitteln:
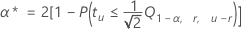
Notation
| Begriff | Beschreibung |
|---|---|
 | mittlere kleinste Quadrate für die i-te Faktorstufe oder Faktorstufenkombination |
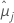 | mittlere kleinste Quadrate für die j-te Faktorstufe oder Faktorstufenkombination |
| r | Anzahl der Mittelwerte |
| Q1 − α, r, u | (1 − α)-Perzentil der Verteilung der studentisierten Spannweiten für r zu vergleichende Mittelwerte mit u Freiheitsgraden |
| u | Freiheitsgrade für Fehler aus dem Modell |
| SEE | Standardfehler der geschätzten Differenz zwischen den mittleren kleinsten Quadraten |
| α | simultane Wahrscheinlichkeit eines Fehlers 1. Art, basierend auf der Verteilung der studentisierten Spannweiten |
| α* | individuelle Wahrscheinlichkeit eines Fehlers 1. Art, basierend auf der t-Verteilung für einen Vergleich |
Literaturhinweise
1 Braun, H. I., Hrsg.(1994). The collected works of John W. Tukey: Volume VIII Multiple comparisons 1948-1983. New York: Chapman and Hall.
2 J. C. Hsu (1996). Multiple Comparisons: Theory and methods. Chapman & Hall.
Fisher-Methode
Formel
Minitab bietet in Bezug auf das Konfidenzintervall verschiedene Methoden zum Vergleichen der Behandlungsmittelwerte. Bei der Fisher-Methode sind Endpunkte des Konfidenzintervalls und p-Werte identisch, unabhängig davon, ob die Vergleiche paarweise oder mit einer Kontrolle erfolgen. Die Fisher-Methode beruht auf dem individuellen Konfidenzniveau. Die Formel für die Konfidenzintervalle lautet wie folgt:
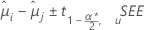
Die Formel für die Teststatistik lautet wie folgt:

p-Wert = 2*P{ T u > tu}
Verwenden Sie die folgende Formel, um das simultane Konfidenzniveau anhand der individuellen Irrtumswahrscheinlichkeit zu ermitteln:

Notation
| Begriff | Beschreibung |
|---|---|
 | mittlere kleinste Quadrate für die i-te Faktorstufe oder Faktorstufenkombination |
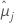 | mittlere kleinste Quadrate für die j-te Faktorstufe oder Faktorstufenkombination |
| t1–α*/2, u | oberes α*/2-Perzentil der Student-t-Verteilung mit u Freiheitsgraden |
| Tu | Zufallsvariable mit einer t-Verteilung mit u Freiheitsgraden für Fehler |
| Q | Zufallsvariable mit einer Verteilung der studentisierten Spannweiten |
| α | simultane Wahrscheinlichkeit eines Fehlers 1. Art |
| α* | individuelle Wahrscheinlichkeit eines Fehlers 1. Art |
| u | Freiheitsgrade für Fehler aus dem Modell |
| SEE | Standardfehler der geschätzten Differenz zwischen den mittleren kleinsten Quadraten |
Bonferroni-Methode
Formel
Minitab bietet in Bezug auf das Konfidenzintervall verschiedene Methoden zum Vergleichen der Behandlungsmittelwerte. Da die Bonferroni-Methode keine Annahmen bezüglich der Abhängigkeit zwischen den Vergleichen macht, ist dies die konservativste Methode. „Konservativ“ bedeutet in diesen Zusammenhang, dass das tatsächliche Konfidenzintervall wahrscheinlich größer als das angezeigte Konfidenzintervall ist. Die Formel für die Konfidenzintervalle lautet wie folgt:
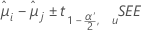
Die Formel für die Teststatistik lautet wie folgt:

Notation
| Begriff | Beschreibung |
|---|---|
 | mittlere kleinste Quadrate für die i-te Faktorstufe oder Faktorstufenkombination |
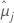 | mittlere kleinste Quadrate für die j-te Faktorstufe oder Faktorstufenkombination |
| t1–α*/2, u | oberes α' /2-Perzentil der Student-t-Verteilung mit u Freiheitsgraden |
| α | simultane Wahrscheinlichkeit eines Fehlers 1. Art |
| α' | α / c |
| c | Anzahl der Vergleiche |
| u | Freiheitsgrade für Fehler aus dem Modell |
| SEE | Standardfehler der geschätzten Differenz zwischen den mittleren kleinsten Quadraten |
Die Anzahl der Vergleiche hängt davon ab, ob die Vergleiche paarweise oder mit einer Kontrolle erfolgen. Sei k die Anzahl der zu vergleichenden Mittelwerte. Die Anzahl der Vergleiche befindet sich in der nachfolgenden Tabelle.
| Paarweise | k (k – 1) / 2 |
| Mit einer Kontrolle | k – 1 |
Sidak-Methode
Formel
Minitab bietet in Bezug auf das Konfidenzintervall verschiedene Methoden zum Vergleichen der Behandlungsmittelwerte. Bei der Sidak-Methode werden die Vergleiche behandelt, als wären diese unabhängig, was zu einer konservativen Approximation der tatsächlichen Fehlerrate führt. Die Sidak-Methode ist etwas trennschärfer als die Bonferroni-Methode.
Die Formel für die Konfidenzintervalle lautet wie folgt:
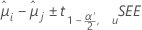
Die Formel für die Teststatistik lautet wie folgt:

Korrigierter p-Wert = 1 − (1 − p)c.
Notation
| Begriff | Beschreibung |
|---|---|
 | mittlere kleinste Quadrate für die i-te Faktorstufe oder Faktorstufenkombination |
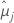 | mittlere kleinste Quadrate für die j-te Faktorstufe oder Faktorstufenkombination |
| t1–α*/2, u | oberes α' /2-Perzentil der Student-t-Verteilung mit u Freiheitsgraden |
| α | simultane Wahrscheinlichkeit eines Fehlers 1. Art |
| α' | 1 – (1 – α ) 1/ k |
| u | Freiheitsgrade für Fehler aus dem Modell |
| SEE | Standardfehler der geschätzten Differenz zwischen den mittleren kleinsten Quadraten |
| p | Nicht korrigierter p-Wert aus der t-Verteilung für einen Vergleich |
| c | Anzahl der Vergleiche |
Die Anzahl der Vergleiche hängt davon ab, ob die Vergleiche paarweise oder mit einer Kontrolle erfolgen. Sei k die Anzahl der Faktorkombinationen. Die Anzahl der Vergleiche befindet sich in der nachfolgenden Tabelle.
| Paarweise | k (k – 1) / 2 |
| Mit einer Kontrolle | k – 1 |
Dunnett-Methode
Formel
Minitab bietet in Bezug auf das Konfidenzintervall verschiedene Methoden zum Vergleichen der Behandlungsmittelwerte. Die Dunnett-Methode ist für Vergleiche mit einer Kontrolle verfügbar. Die Formel für die Konfidenzintervalle lautet wie folgt:

Die Formel für die Teststatistik lautet wie folgt:

Der korrigierte p-Wert ist das Ergebnis der Integration der Verteilung, die Dunnett für die Teststatistik vorschlägt. Einzelheiten finden Sie in den unten aufgeführten Veröffentlichungen.
Notation
| Begriff | Beschreibung |
|---|---|
 | mittlere kleinste Quadrate für die i-te Faktorstufe oder Faktorstufenkombination |
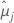 | mittlere kleinste Quadrate für die j-te Faktorstufe oder Faktorstufenkombination |
| D1–α, k–1, u | oberes α-Perzentil der von Dunnett vorgeschlagenen Verteilung mit k – 1 Vergleichen und u Freiheitsgraden |
| α | simultane Wahrscheinlichkeit eines Fehlers 1. Art |
| k | Anzahl zu vergleichender Mittelwerte |
| u | Freiheitsgrade für Fehler aus dem Modell |
| SEE | Standardfehler der geschätzten Differenz zwischen den mittleren kleinsten Quadraten |
Literaturhinweise
1 Dunnett, C. W. Nelson (1990). (1. Januar 1955). A multiple comparison procedure for comparing several treatments with a control. Journal of the American Statistical Association, 50, 1096-1121.
2 J. C. Hsu (1996). Multiple Comparisons: Theory and methods. Chapman & Hall.
