In diesem Thema
- Dunnett-Methode für Vergleiche mit einer Kontrolle in einem Modell mit gemischten Effekten
- Fisher-Methode für Vergleiche mit einer Kontrolle in einem Modell mit gemischten Effekten
- Bonferroni-Methode für Vergleiche mit einer Kontrolle in einem Modell mit gemischten Effekten
- Sidak-Methode für Vergleiche mit einer Kontrolle in einem Modell mit gemischten Effekten
Dunnett-Methode für Vergleiche mit einer Kontrolle in einem Modell mit gemischten Effekten
Bei Mehrfachvergleichen mit einer Kontrolle berechnet Minitab außerdem einseitige Intervalle.
- Obergrenze
- Untergrenze
Weitere Informationen zur Berechnung der angepassten Mittelwerte und des Standardfehlers der Differenz finden Sie unter Methoden und Formeln für angepasste Mittelwerte in Modell mit gemischten Effekten anpassen.
Hinweis
Die Berechnungen für die Teststatistik, den korrigierten p-Wert, das individuelle Konfidenzniveau und die Tabelle der Gruppierungsinformationen stimmen mit den Berechnungen für allgemeine lineare Modelle überein. Weitere Informationen finden Sie in den Methoden und Formeln für Vergleiche bei allgemeinen linearen Modellen.
Kritischer Wert
- Dunnett, C. W. (1. Januar 1955). A multiple comparison procedure for comparing several treatments with a control. Journal of the American Statistical Association, 50, 1096-1121.
- J.C. Hsu (1996). Multiple Comparisons: Theory and methods. Chapman & Hall.
| Begriff | Beschreibung |
|---|---|
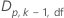 | oberes  -Perzentil der von Dunnett vorgeschlagenen Verteilung mit  Vergleichen und df Freiheitsgraden |
| α | simultane Wahrscheinlichkeit eines Fehlers 1. Art |
| k | Anzahl der Stufen im Term mit festen Effekten oder im Zufallsterm |
| df | Freiheitsgrade |
Die Freiheitsgrade hängen davon ab, ob der Vergleich für einen Term mit festen Effekten oder einen Zufallsterm erfolgt.
Freiheitsgrade (df)
Bei einem Term mit festen Effekten entsprechen die Freiheitsgrade (df) den Freiheitsgraden für den Test des entsprechenden Terms mit festen Effekten. Bei einem Zufallsterm wird für die Freiheitsgrade die Satterthwaite-Approximationsmethode verwendet.
Weitere Informationen zur Berechnung der Freiheitsgrade finden Sie unter Methoden und Formeln für Tests auf feste Effekte in Modell mit gemischten Effekten anpassen.
Fisher-Methode für Vergleiche mit einer Kontrolle in einem Modell mit gemischten Effekten
Bei Mehrfachvergleichen mit einer Kontrolle berechnet Minitab außerdem einseitige Intervalle.
- Obergrenze
- Untergrenze
Weitere Informationen zur Berechnung der angepassten Mittelwerte und des Standardfehlers der Differenz finden Sie unter Methoden und Formeln für angepasste Mittelwerte in Modell mit gemischten Effekten anpassen.
Hinweis
Die Berechnungen für die Teststatistik, den korrigierten p-Wert, das individuelle Konfidenzniveau und die Tabelle der Gruppierungsinformationen stimmen mit den Berechnungen für allgemeine lineare Modelle überein. Weitere Informationen finden Sie in den Methoden und Formeln für Vergleiche bei allgemeinen linearen Modellen.
Kritischer Wert
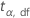
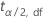
| Begriff | Beschreibung |
|---|---|
 |  Quantil der Student-t-Verteilung mit df Freiheitsgraden |
| α | individuelle Wahrscheinlichkeit eines Fehlers 1. Art |
| df | Freiheitsgrade |
Die Freiheitsgrade hängen davon ab, ob der Vergleich für einen Term mit festen Effekten oder einen Zufallsterm erfolgt.
Freiheitsgrade (df)
Bei einem Term mit festen Effekten entsprechen die Freiheitsgrade (df) den Freiheitsgraden für den Test des entsprechenden Terms mit festen Effekten. Bei einem Zufallsterm wird für die Freiheitsgrade die Satterthwaite-Approximationsmethode verwendet.
Weitere Informationen zur Berechnung der Freiheitsgrade finden Sie unter Methoden und Formeln für Tests auf feste Effekte in Modell mit gemischten Effekten anpassen.
Bonferroni-Methode für Vergleiche mit einer Kontrolle in einem Modell mit gemischten Effekten
Bei Mehrfachvergleichen mit einer Kontrolle berechnet Minitab außerdem einseitige Intervalle.
- Obergrenze
- Untergrenze
Weitere Informationen zur Berechnung der angepassten Mittelwerte und des Standardfehlers der Differenz finden Sie unter Methoden und Formeln für angepasste Mittelwerte in Modell mit gemischten Effekten anpassen.
Hinweis
Die Berechnungen für die Teststatistik, den korrigierten p-Wert, das individuelle Konfidenzniveau und die Tabelle der Gruppierungsinformationen stimmen mit den Berechnungen für allgemeine lineare Modelle überein. Weitere Informationen finden Sie in den Methoden und Formeln für Vergleiche bei allgemeinen linearen Modellen.
Kritischer Wert
| Begriff | Beschreibung |
|---|---|
 | oberes  Perzentil der Student-t-Verteilung mit df Freiheitsgraden |
| α | simultane Wahrscheinlichkeit eines Fehlers 1. Art |
| c |  |
| k | Anzahl der Stufen im Term mit festen Effekten oder im Zufallsterm |
| df | Freiheitsgrade |
Die Freiheitsgrade hängen davon ab, ob der Vergleich für einen Term mit festen Effekten oder einen Zufallsterm erfolgt.
Freiheitsgrade (df)
Bei einem Term mit festen Effekten entsprechen die Freiheitsgrade (df) den Freiheitsgraden für den Test des entsprechenden Terms mit festen Effekten. Bei einem Zufallsterm wird für die Freiheitsgrade die Satterthwaite-Approximationsmethode verwendet.
Weitere Informationen zur Berechnung der Freiheitsgrade finden Sie unter Methoden und Formeln für Tests auf feste Effekte in Modell mit gemischten Effekten anpassen.
Sidak-Methode für Vergleiche mit einer Kontrolle in einem Modell mit gemischten Effekten
Bei Mehrfachvergleichen mit einer Kontrolle berechnet Minitab außerdem einseitige Intervalle.
- Obergrenze
- Untergrenze
Weitere Informationen zur Berechnung der angepassten Mittelwerte und des Standardfehlers der Differenz finden Sie unter Methoden und Formeln für angepasste Mittelwerte in Modell mit gemischten Effekten anpassen.
Hinweis
Die Berechnungen für die Teststatistik, den korrigierten p-Wert, das individuelle Konfidenzniveau und die Tabelle der Gruppierungsinformationen stimmen mit den Berechnungen für allgemeine lineare Modelle überein. Weitere Informationen finden Sie in den Methoden und Formeln für Vergleiche bei allgemeinen linearen Modellen.
Kritischer Wert
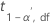
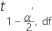
| Begriff | Beschreibung |
|---|---|
 | oberes  Perzentil der Student-t-Verteilung mit df Freiheitsgraden |
 |  |
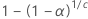| α | simultane Wahrscheinlichkeit eines Fehlers 1. Art |
| c |  |
| k | Anzahl der Stufen im Term mit festen Effekten oder im Zufallsterm |
| df | Freiheitsgrade |
Die Freiheitsgrade hängen davon ab, ob der Vergleich für einen Term mit festen Effekten oder einen Zufallsterm erfolgt.
Freiheitsgrade (df)
Bei einem Term mit festen Effekten entsprechen die Freiheitsgrade (df) den Freiheitsgraden für den Test des entsprechenden Terms mit festen Effekten. Bei einem Zufallsterm wird für die Freiheitsgrade die Satterthwaite-Approximationsmethode verwendet.
Weitere Informationen zur Berechnung der Freiheitsgrade finden Sie unter Methoden und Formeln für Tests auf feste Effekte in Modell mit gemischten Effekten anpassen.
