Was sind die Niveau- und die Trendkomponente bei der zweifachen exponentiellen Glättung?

Bei der zweifachen exponentiellen Glättung werden für jede Periode eine Niveaukomponente und eine Trendkomponente verwendet. Es werden zwei Gewichtungen bzw. Glättungsparameter verwendet, um die Komponenten für jede Periode zu aktualisieren. Die Gleichungen für die zweifache exponentielle Glättung lauten wie folgt:

L_t = α Y_t + (1 – α) [L_t–1 + T_t–1]
T_t = γ[L_t – L_t–1] + (1 – γ) T_t–1
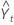= L_t–1 + T_t–1

Hierbei ist L_t das Niveau zum Zeitpunkt t, α ist die Gewichtung für das Niveau, T_t ist der Trend zum Zeitpunkt t, γ ist die Gewichtung für den Trend, Y_t ist der Datenwert zum Zeitpunkt t, und 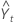ist der angepasste Wert bzw. die Prognose für eine Periode im Voraus zum Zeitpunkt t.

Die erste Beobachtung wird mit 1 nummeriert, und dann müssen die Niveau- und Trendschätzungen zum Zeitpunkt null initialisiert werden, um fortfahren zu können. Die verwendete Initialisierungsmethode bestimmt, mit welchem von zwei Verfahren die geglätteten Werte ermittelt werden: mit Gewichtungen, die von Minitab generiert werden, oder mit angegebenen Gewichtungen.

Optimale ARIMA-Gewichtungen	Angegebene Gewichtungen
Minitab passt ein ARIMA(0;2;2)-Modell an die Daten an, mit dem die Summe der quadrierten Fehler minimiert wird. Die Trend- und die Niveaukomponente werden anschließend per Rückwärtsprognose initialisiert.	Minitab passt ein lineares Regressionsmodell an die Zeitreihendaten (y-Variable) im Vergleich mit der Zeit (x-Variable) an. Die Konstante (Schnittpunkt mit der y-Achse) aus dieser Regression ist die Anfangsschätzung der Niveaukomponente, der Steigungskoeffizient die Anfangsschätzung der Trendkomponente.

Wenn Sie Gewichtungen angeben, die einem ARIMA(0;2;2)-Modell mit gleichen Wurzeln entsprechen, entspricht die Holt-Methode der spezifischeren Brown-Methode.