Minitab bietet verschiedene Analysen, mit deren Hilfe Zeitreihen ausgewertet werden können. Zu diesen Analysen zählen einfache Prognose- und Glättungsmethoden, Methoden zum Analysieren der Korrelation und die ARIMA-Modellierung. Prinzipiell kann Korrelationsanalyse zwar auch getrennt von der ARIMA-Modellierung durchgeführt werden, in Minitab werden die Methoden zur Analyse der Korrelation jedoch im Rahmen der ARIMA-Modellierung angeboten.
Einfache Prognose- und Glättungsmethoden
Mit den einfachen Prognose- und Glättungsmethoden werden Komponenten in einer Zeitreihe modelliert, die in einem Zeitreihendiagramm der Daten gewöhnlich leicht zu beobachten sind. Bei diesem Ansatz werden die Daten in ihre Komponenten zerlegt, und anschließend werden die Schätzwerte der Komponenten in die Zukunft extrapoliert, um Prognosen zu erstellen. Sie können statische Methoden der Trendanalyse und Zerlegung oder dynamische Methoden gleitender Durchschnitte, einfache und zweifache exponentielle Glättung sowie die Winters-Methode auswählen. Statische Methoden behandeln Muster, die sich nicht mit der Zeit ändern; dynamische Methoden behandeln Muster, die sich mit der Zeit ändern, und die Schätzwerte werden anhand von benachbarten Werten aktualisiert.
Sie können zwei Methoden gemeinsam verwenden. Das bedeutet, dass Sie eine Komponente mit einer statischen Methode und eine andere Komponente mit einer dynamischen Methode modellieren können. Beispielsweise können Sie einen statischen Trend mit der Trendanalyse anpassen und die Saisonkomponente in den Residuen mit der Winters-Methode dynamisch modellieren. Sie können auch ein statisches Modell mit Saisonkomponente durch Zerlegung anpassen und die Trendkomponente in den Residuen durch zweifache exponentielle Glättung dynamisch modellieren. Zudem können Sie eine Trendanalyse und Zerlegung gemeinsam anwenden, so dass Sie die größere Auswahl an Trendmodellen nutzen können, die durch die Trendanalyse geboten wird. Die gemeinsame Verwendung von Methoden weist den Nachteil auf, dass die Konfidenzintervalle für Prognosen nicht gültig sind.
Die folgende Tabelle enthält für jede Methode eine Zusammenfassung sowie eine Grafik von Anpassungen und Prognosen gängiger Daten.
Trendanalyse
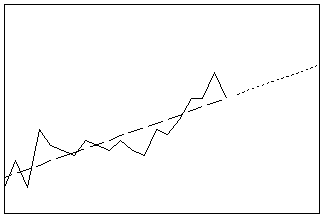
Passt ein allgemeines Trendmodell an Zeitreihendaten an. Sie können zwischen linearen, quadratischen, exponentiellen Wachstums- oder Rückgangs- sowie S-Kurven-Trendmodellen auswählen. Passen Sie Trends mit diesem Verfahren an, wenn die Zeitreihen keine Saisonkomponente aufweisen.
- Länge: lang
- Profil: Verlängerung der Trendlinie
Zerlegung
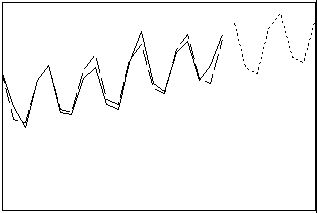
Teilt die Zeitreihe in eine lineare Trendkomponente, eine Saisonkomponente und eine Fehlerkomponente auf. Wählen Sie aus, ob die Saisonkomponente additiv oder multiplikativ in Bezug auf den Trend ist. Verwenden Sie dieses Verfahren für Prognosen, wenn in der Zeitreihe eine Saisonkomponente vorhanden ist oder wenn Sie die Art der Komponenten untersuchen möchten.
- Länge: lang
- Profil: Trend mit saisonalem Muster
Gleitender Durchschnitt
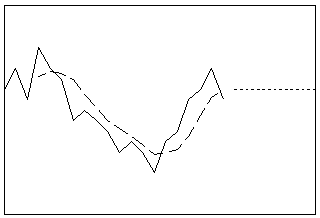
Glättet die Daten durch Berechnen des Durchschnitts von aufeinander folgenden Beobachtungen in einer Zeitreihe. Sie können dieses Verfahren verwenden, wenn die Daten keine Trendkomponente aufweisen. Wenn eine saisonale Komponente vorliegt, legen Sie die Länge des gleitenden Durchschnitts auf den gleichen Wert wie die Länge des saisonalen Zyklus fest.
- Länge: kurz
- Profil: waagerechte Linie
Einfache exponentielle Glättung
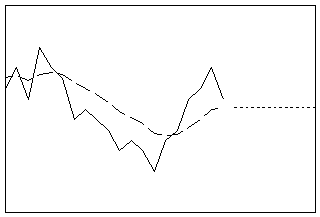
Glättet die Daten mit der optimalen ARIMA(0;1;1)-Prognoseformel für eine Periode im Voraus. Dieses Verfahren eignet sich besonders, wenn weder eine Trend- noch eine Saisonkomponente vorhanden ist. Die einzig dynamische Komponente in einem Modell des gleitenden Durchschnitts ist das Niveau.
- Länge: kurz
- Profil: waagerechte Linie
Zweifache exponentielle Glättung
Glättet die Daten mit der optimalen ARIMA(0;2;2)-Prognoseformel für eine Periode im Voraus. Dieses Verfahren kann gut geeignet sein, wenn ein Trend vorhanden ist, doch kann es auch als allgemeine Glättungsmethode verwendet werden. Bei der zweifachen exponentiellen Glättung werden dynamische Schätzwerte für zwei Komponenten berechnet: Niveau und Trend.
- Länge: kurz
- Profil: Gerade, deren Steigung gleich dem letzten Trendschätzwert ist
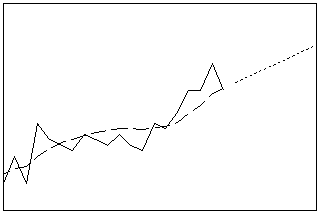
Winters-Methode
Glättet die Daten mit der exponentiellen Glättung nach Holt-Winters. Verwenden Sie dieses Verfahren, wenn eine Trend- und eine Saisonkomponente vorhanden sind und diese beiden Komponenten entweder additiv oder multiplikativ sind. Bei der Winters-Methode werden dynamische Schätzwerte für drei Komponenten berechnet: Niveau, Trend und Saison.
- Länge: kurz- bis mittelfristig
- Profil: Trend mit saisonalem Muster
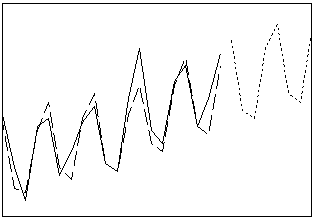
Korrelationsanalyse und ARIMA-Modellierung
In der ARIMA-Modellierung (Autoregressive Integrated Moving Average, autoregressive integrierte gleitende Durchschnitte) werden ebenfalls Muster in den Daten genutzt, die in einem Diagramm der Daten jedoch möglicherweise nicht leicht erkennbar sind. Stattdessen werden in der ARIMA-Modellierung Differenzbildung sowie die Autokorrelationsfunktion und die partielle Autokorrelationsfunktion verwendet, um ein akzeptables Modell zu ermitteln.
Mit der ARIMA-Modellierung können viele unterschiedliche Zeitreihen mit und ohne Trend- oder Saisonkomponente modelliert sowie Prognosen erstellt werden. Das Prognoseprofil hängt vom angepassten Modell ab. Im Vergleich zu den einfachen Prognose- und Glättungsmethoden bietet die ARIMA-Modellierung den Vorteil, dass Modelle hierbei flexibler an die Daten angepasst werden können. Das Ermitteln und Anpassen eines Modells kann jedoch zeitaufwändig sein, und die ARIMA-Modellierung lässt sich nicht einfach automatisieren.
- Differenzen
- Berechnet und speichert die Differenzen zwischen den Datenwerten einer Zeitreihe. Wenn Sie ein ARIMA-Modell anpassen möchten, die vorliegenden Daten jedoch eine Trend- oder Saisonkomponente enthalten, ist die Differenzbildung für die Daten ein gängiger Schritt bei der Untersuchung wahrscheinlicher ARIMA-Modelle. Mit der Differenzbildung wird die Korrelationsstruktur vereinfacht und ggf. das zugrunde liegende Muster aufgezeigt.
- Lag
- Berechnet und speichert die Lags einer Zeitreihe. Wenn Sie die Lags einer Zeitreihe berechnen, verschiebt Minitab die ursprünglichen Werte in der Spalte nach unten und fügt fehlende Werte am Anfang der Spalte ein. Die Anzahl der eingefügten fehlenden Werte hängt von der Länge des Lags ab.
- Autokorrelation
- Berechnet und erstellt ein Diagramm der Autokorrelationen einer Zeitreihe. Bei der Autokorrelation handelt es sich um die Korrelation zwischen den durch k Zeiteinheiten getrennten Beobachtungen in einer Zeitreihe. Die grafische Darstellung der Autokorrelationen wird als Autokorrelationsfunktion (ACF) bezeichnet. Betrachten Sie die ACF, um die in ein ARIMA-Modell aufzunehmenden Terme auszuwählen.
- Partielle Autokorrelation
- Berechnet und erstellt ein Diagramm der partiellen Autokorrelationen einer Zeitreihe. Mit partiellen Autokorrelationen werden wie mit Autokorrelationen Gruppen geordneter Datenpaare einer Zeitreihe korreliert. Partielle Autokorrelationen messen wie partielle Korrelationen bei der Regression die Stärke der Beziehung zu anderen Termen, die erklärt werden. Die partielle Autokorrelation bei einem Lag k ist die Korrelation zwischen den Residuen zum Zeitpunkt t aus einem autoregressiven Modell und den Beobachtungen bei Lag k mit Termen für alle dazwischen liegenden Lags im autoregressiven Modell. Die grafische Darstellung der partiellen Autokorrelationen wird als partielle Autokorrelationsfunktion (PACF) bezeichnet. Betrachten Sie die PACF, um die in ein ARIMA-Modell aufzunehmenden Terme auszuwählen.
- Kreuzkorrelation
- Berechnet und erstellt ein Diagramm der Korrelationen zwischen zwei Zeitreihen.
- ARIMA
- Passt ein Box-Jenkins-ARIMA-Modell an eine Zeitreihe an. Die einzelnen Begriffe im Namen ARIMA – „autoregressiv“, „integriert“ und „gleitende Durchschnitte“ – stellen die Filterschritte dar, mit denen das ARIMA-Modell berechnet wird, bis nur noch Zufallsrauschen übrig bleibt. Mit Hilfe der ARIMA können Sie das Verhalten von Zeitreihen modellieren und Prognosen erstellen.
