Support für Minitab® 

Methoden und Formeln für Winters-Methode

Weitere Informationen zu Minitab
Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Multiplikativ

Formel

Das multiplikative Modell lautet wie folgt:

  • Lt = α (Yt / St–p) + (1 – α) [Lt–1 + Tt–1]
  • Tt = γ [Lt – Lt–1] + (1 – γ) Tt–1
  • St = δ (Yt / Lt) + (1 – δ) St–p
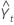  • = (Lt–1 + Tt–1) St–p

Notation

BegriffBeschreibung
LtNiveau zum Zeitpunkt t, α ist die Gewichtung für das Niveau
TtTrend zum Zeitpunkt t,
γGewichtung für den Trend
StSaisonkomponente zum Zeitpunkt t
δGewichtung für die Saisonkomponente
psaisonale Periode
YtDatenwert zum Zeitpunkt t
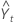angepasster Wert bzw. die Prognose für eine Periode im Voraus zum Zeitpunkt t

Methode zur Berechnung von Anfangswerten für Niveau und Trend für multiplikative Modelle

Die folgende Methode setzt eine saisonale Länge größer als 4 voraus.

  1. Finden Sie den Mittelwert, das Minimum und das Maximum der Daten. Für dieses Beispiel gilt Folgendes:
    • Mittelwert = 554,208
    • Min = 1
    • Max = 1498,47
  2. Berechnen Sie für jede Datenzeile:
  3. N sei gleich der saisonalen Länge. Für dieses Beispiel ist N = 12.
  4. Führen Sie die Regression mit den ersten N „Temp-Werten“ (berechnet in Schritt 2) als Y-Variable und einem Vektor von 1 bis N als X-Variable aus. Also gilt für dieses Beispiel Folgendes:
    Y X
    4104,36 1
    4104,36 2
    4630,36 3
    4922,80 4
    4822,40 5
    5601,83 6
    4891,77 7
    4604,44 8
    4411,26 9
    4123,66 10
    4104,36 11
    4104,36 12

    Die Steigung der Regressionslinie ist der Anfangswert für den Trend.

  5. Passen Sie den Achsenabschnitt für die Regressionslinie an, indem Sie Folgendes subtrahieren:

Der Achsenabschnitt für die Daten beträgt 4705,24. Subtrahieren Sie 4103,36 vom Achsenabschnitt, um einen angepassten Achsenabschnitt von 601,879 zu erhalten. Dieser angepasste Achsenabschnitt ist der Anfangswert für das Niveau.

Zusatz

Formel

Das additive Modell lautet wie folgt:
  • Lt = α (Yt – St–p) + (1 – α) [Lt–1 + Tt–1]
  • Tt = γ [Lt – Lt–1] + (1 – γ) Tt–1
  • St = δ (Yt – Lt) + (1 – δ) St–p
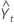  • = Lt–1 + Tt–1 + St–p

Notation

BegriffBeschreibung
LtNiveau zum Zeitpunkt t, α ist die Gewichtung für das Niveau
TtTrend zum Zeitpunkt t,
γGewichtung für den Trend
StSaisonkomponente zum Zeitpunkt t
δGewichtung für die Saisonkomponente
psaisonale Periode
YtDatenwert zum Zeitpunkt t
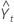angepasster Wert bzw. die Prognose für eine Periode im Voraus zum Zeitpunkt t

Methode zur Berechnung von Anfangswerten für Niveau und Trend für additive Modelle

Die folgende Methode setzt eine saisonale Länge größer als 4 voraus.

  1. N sei gleich der saisonalen Länge. Für dieses Beispiel ist N = 12.
  2. Führen Sie die Regression mit den ersten N Datenwerten als y-Variable und einem Vektor von 1 bis N als x-Variable aus. Also gilt für dieses Beispiel Folgendes:
    Y X
    1,00 1
    1,00 2
    527,00 3
    819,45 4
    719,04 5
    1498,47 6
    788,42 7
    501,08 8
    307,90 9
    20,30 10
    1,00 11
    1,00 12

    Die Steigung der Regressionslinie ist der Anfangswert für den Trend. Der Schnittpunkt der Regressionslinie mit der y-Achse ist der Anfangswert für die Stufe.

Methode zur Berechnung von Anfangswerten für saisonale Indizes für additive Modelle

Die folgende Methode setzt eine saisonale Länge größer als 4 voraus.

  1. Führen Sie die Regression mit den Datenwerten als y-Variable und einem Vektor von 1 bis 24 als x-Variable aus. Also gilt für dieses Beispiel Folgendes:
    Y X
    1,00 1
    1,00 2
    527,00 3
    819,45 4
    719,04 5
    1498,47 6
    788,42 7
    501,08 8
    307,90 9
    20,30 10
    1,00 11
    1,00 12
    83,00 13
    668,21 14
    1121,28 15
    1386,84 16
    1031,18 17
    988,60 18
    1380,30 19
    1005,97 20
    233,69 21
    211,87 22
    2,00 23
    2,40 24

    Verwenden Sie die Residuen aus diesem Regressionsmodell im nächsten Schritt

  2. Führen Sie die Regression mit den Residuen als y-Variable und 12 Indikatorvariablen (z.1 bis z.12) als x-Variablen aus. Passen Sie das Regressionsmodell ohne einen (konstanten) Term für den Schnittpunkt mit der y-Achse an. Also gilt für dieses Beispiel Folgendes:
    Residuen z.1 z.2 z.3 z.4 z.5 z.6 z.7 z.8 z.9 z.10 z.11 z.12
    -508,261 1 0 0 0 0 0 0 0 0 0 0 0
    -512,170 0 1 0 0 0 0 0 0 0 0 0 0
    9,926 0 0 1 0 0 0 0 0 0 0 0 0
    298,460 0 0 0 1 0 0 0 0 0 0 0 0
    194,145 0 0 0 0 1 0 0 0 0 0 0 0
    969,667 0 0 0 0 0 1 0 0 0 0 0 0
    255,705 0 0 0 0 0 0 1 0 0 0 0 0
    -35,538 0 0 0 0 0 0 0 1 0 0 0 0
    -232,625 0 0 0 0 0 0 0 0 1 0 0 0
    -524,137 0 0 0 0 0 0 0 0 0 1 0 0
    -547,346 0 0 0 0 0 0 0 0 0 0 1 0
    -551,254 0 0 0 0 0 0 0 0 0 0 0 1
    -473,161 1 0 0 0 0 0 0 0 0 0 0 0
    108,141 0 1 0 0 0 0 0 0 0 0 0 0
    557,303 0 0 1 0 0 0 0 0 0 0 0 0
    818,952 0 0 0 1 0 0 0 0 0 0 0 0
    459,378 0 0 0 0 1 0 0 0 0 0 0 0
    412,890 0 0 0 0 0 1 0 0 0 0 0 0
    800,684 0 0 0 0 0 0 1 0 0 0 0 0
    422,451 0 0 0 0 0 0 0 1 0 0 0 0
    -353,739 0 0 0 0 0 0 0 0 1 0 0 0
    -379,468 0 0 0 0 0 0 0 0 0 1 0 0
    -593,247 0 0 0 0 0 0 0 0 0 0 1 0
    Die Koeffizienten aus diesem Regressionsmodell sind die Anfangswerte für die saisonalen Indizes. Die Koeffizienten sind:
    Punkt COEF1
    1 -490,711
    2 -202,014
    3 283,615
    4 558,706
    5 326,762
    6 691,278
    7 528,195
    8 193,456
    9 -293,182
    10 -451,803
    11 -570,297
    12 -574,005
    Hinweis

    Die Indikatorvariablen z.1 bis z.12 geben an, zu welchem Monat der Periode jeder Datenpunkt gehört. Beispielsweise ist die Variable z.1 für den ersten Monat der Periode gleich 1 und andernfalls gleich 0.

Modellanpassung

Bei der Winters-Methode werden für jede Periode eine Niveaukomponente, eine Trendkomponente und eine Saisonkomponente verwendet. Es werden drei Gewichtungen bzw. Glättungsparameter verwendet, um die Komponenten für jede Periode zu aktualisieren. Die Anfangswerte für die Niveau- und die Trendkomponente werden aus einer linearen Regression auf die Zeit ermittelt. Die Anfangswerte für die Saisonkomponente werden mit Hilfe trendbereinigter Daten aus einer Regression mit Dummy-Variable ermittelt.

Prognosen

Bei der Winters-Methode werden Prognosen anhand der Niveau-, der Trend- und der Saisonkomponente erstellt. Des Weiteren werden bei der Winters-Methode zum Erstellen der Prognosen Daten bis zur Zeit des Prognoseursprungs verwendet.

Formel

Die Prognose für m Perioden ab einem bestimmten Zeitpunkt t lautet wie folgt:
  • Multiplikative Methode: (Lt + mTt) * St + m –p
  • Additive Methode: Lt + mTt +St + m –p

Notation

BegriffBeschreibung
Lt Niveau
Tt Trend zum Zeitpunkt t
BegriffBeschreibung
St + m −pSaisonkomponente für die gleiche Periode des Vorjahres

MAPE

Der mittlere absolute prozentuale Fehler (MAPE) ist eine Maßzahl für die Genauigkeit der angepassten Zeitreihenwerte. MAPE drückt die Genauigkeit als Prozentsatz aus.

Formel

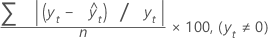
Notation

BegriffBeschreibung
yt tatsächlicher Wert zum Zeitpunkt t
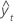angepasster Wert
n Anzahl der Beobachtungen

MAD

Die mittlere absolute Abweichung (MAD) ist eine Maßzahl für die Genauigkeit der angepassten Zeitreihenwerte. MAD drückt die Genauigkeit in der gleichen Einheit wie die Daten aus, wodurch der Fehlerbetrag leichter erfasst werden kann.

Formel

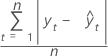
Notation

BegriffBeschreibung
yt tatsächlicher Wert zum Zeitpunkt t
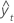angepasster Wert
n Anzahl der Beobachtungen

MSD

Die mittlere quadrierte Abweichung (MSD) wird immer mit demselben Nenner n berechnet, unabhängig vom Modell. MSD ist bei ungewöhnlich großen Prognosefehlern ein empfindlicheres Maß als MAD.

Formel

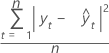
Notation

BegriffBeschreibung
yt tatsächlicher Wert zum Zeitpunkt t
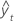angepasster Wert
n Anzahl der Beobachtungen
Copyright © 2025 Minitab, LLC. All rights Reserved.