In diesem Thema
Länge
Die Anzahl der Beobachtungen in der Zeitreihe.
α (Niveau)
α ist die Gewichtung, die für die Niveaukomponente der geglätteten Schätzung verwendet wird. α ist mit einem gleitenden Durchschnitt der Beobachtungen vergleichbar. Mit den Gewichtungen wird der Grad der Glättung angepasst, indem festgelegt wird, wie die einzelnen Komponenten auf aktuelle Bedingungen reagieren. Bei einer niedrigeren Gewichtung erhalten neuere Daten weniger Gewicht. Bei einer höheren Gewichtung erhalten neuere Daten mehr Gewicht. Beim Anpassen von Gewichtungen führt eine Anpassung der Gewichtung für die Niveaukomponente häufig am ehesten zu besseren Genauigkeitsmaßen. Eine Änderung der anderen Gewichtungen hat meist nur geringe Auswirkungen, nachdem Sie die Gewichtung des Niveaus wie gewünscht angepasst haben.
γ (Trend)
Höhere Gewichtungen vergrößern den Einfluss neuerer Daten, so dass die Prognosen (grün) dem Abwärtstrend am Ende der Daten (schwarz) folgen.
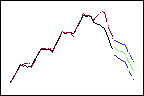
Höhere Gewichtung für den Trend
Niedrigere Gewichtungen verringern den Einfluss neuerer Daten, so dass die Prognosen dem allgemeinen Aufwärtstrend folgen.
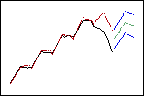
Niedrigere Gewichtung für den Trend
δ (saisonal)
δ ist die Gewichtung für die Saisonkomponente der geglätteten Schätzung. Mit den Gewichtungen wird der Grad der Glättung angepasst, indem festgelegt wird, wie die einzelnen Komponenten auf aktuelle Bedingungen reagieren. Bei einer niedrigeren Gewichtung erhalten neuere Daten weniger Gewicht. Bei einer höheren Gewichtung erhalten neuere Daten mehr Gewicht.
MAPE
Der mittlere absolute prozentuale Fehler (MAPE) drückt die Genauigkeit als Prozentsatz des Fehlers aus. Da es sich bei MAPE um einen Prozentsatz handelt, ist dieser Wert möglicherweise verständlicher als die anderen Genauigkeitsmaße. Wenn der MAPE-Wert beispielsweise 5 beträgt, weicht die Prognose im Durchschnitt um 5 % ab.
In einigen Fällen kann jedoch ein sehr großer MAPE-Wert auftreten, obwohl das Modell gut an die Daten angepasst zu sein scheint. Untersuchen Sie das Diagramm auf Datenwerte, die nah bei 0 liegen. Da beim MAPE der absolute Fehler durch die tatsächlichen Daten dividiert wird, können Werte, die nah bei 0 liegen, den MAPE stark ansteigen lassen.
Interpretation
Verwenden Sie dieses Maß, um die Anpassungen verschiedener Zeitreihenmodelle zu vergleichen. Kleiner Werte weisen auf eine bessere Anpassung hin. Wenn ein einzelnes Modell nicht die kleinsten Werte für alle 3 Genauigkeitsmaße aufweist, ist MAPE in der Regel die bevorzugte Maßzahl.
Die Genauigkeitsmaße basieren auf Residuen für eine Periode im Voraus. Das Modell wird verwendet, um an jedem Zeitpunkt den y-Wert für die nächste Periode zu prognostizieren. Die Differenzen zwischen den prognostizierten Werten (Anpassungen) und dem jeweils tatsächlichen y-Wert sind die Residuen für eine Periode im Voraus. Aus diesem Grund liefern die Genauigkeitsmaße einen Hinweis auf die Genauigkeit, die Sie erwarten können, wenn Sie am Ende der Daten eine Periode in die Zukunft prognostizieren. Sie geben daher nicht die Genauigkeit von Prognosen an, die weiter als eine Periode in der Zukunft liegen. Wenn Sie das Modell für Prognosen verwenden, sollte Ihre Entscheidung nicht ausschließlich auf den Genauigkeitsmaßen basieren. Sie sollten auch die Anpassung des Modells untersuchen, um sicherzustellen, dass die Prognosen und das Modell eng an den Daten liegen, insbesondere am Ende der Datenreihe.
MAD
Die mittlere absolute Abweichung (MAD) drückt die Genauigkeit in der gleichen Einheit wie die Daten aus. Auf diese Weise kann der Fehleranteil leichter erfasst werden. Ausreißer haben eine geringere Auswirkung auf MAD als auf MSD.
Interpretation
Verwenden Sie dieses Maß, um die Anpassungen verschiedener Zeitreihenmodelle zu vergleichen. Kleinere Werte weisen auf eine bessere Anpassung hin.
Die Genauigkeitsmaße basieren auf Residuen für eine Periode im Voraus. Das Modell wird verwendet, um an jedem Zeitpunkt den y-Wert für die nächste Periode zu prognostizieren. Die Differenzen zwischen den prognostizierten Werten (Anpassungen) und dem jeweils tatsächlichen y-Wert sind die Residuen für eine Periode im Voraus. Aus diesem Grund liefern die Genauigkeitsmaße einen Hinweis auf die Genauigkeit, die Sie erwarten können, wenn Sie am Ende der Daten eine Periode in die Zukunft prognostizieren. Sie geben daher nicht die Genauigkeit von Prognosen an, die weiter als eine Periode in der Zukunft liegen. Wenn Sie das Modell für Prognosen verwenden, sollte Ihre Entscheidung nicht ausschließlich auf den Genauigkeitsmaßen basieren. Sie sollten auch die Anpassung des Modells untersuchen, um sicherzustellen, dass die Prognosen und das Modell eng an den Daten liegen, insbesondere am Ende der Datenreihe.
MSD
Die mittlere quadrierte Abweichung (MSD) ist eine Maßzahl für die Genauigkeit der angepassten Zeitreihenwerte. Ausreißer haben eine stärkere Auswirkung auf MSD als auf MAD.
Interpretation
Verwenden Sie dieses Maß, um die Anpassungen verschiedener Zeitreihenmodelle zu vergleichen. Kleinere Werte weisen auf eine bessere Anpassung hin.
Die Genauigkeitsmaße basieren auf Residuen für eine Periode im Voraus. Das Modell wird verwendet, um an jedem Zeitpunkt den y-Wert für die nächste Periode zu prognostizieren. Die Differenzen zwischen den prognostizierten Werten (Anpassungen) und dem jeweils tatsächlichen y-Wert sind die Residuen für eine Periode im Voraus. Aus diesem Grund liefern die Genauigkeitsmaße einen Hinweis auf die Genauigkeit, die Sie erwarten können, wenn Sie am Ende der Daten eine Periode in die Zukunft prognostizieren. Sie geben daher nicht die Genauigkeit von Prognosen an, die weiter als eine Periode in der Zukunft liegen. Wenn Sie das Modell für Prognosen verwenden, sollte Ihre Entscheidung nicht ausschließlich auf den Genauigkeitsmaßen basieren. Sie sollten auch die Anpassung des Modells untersuchen, um sicherzustellen, dass die Prognosen und das Modell eng an den Daten liegen, insbesondere am Ende der Datenreihe.
Glätten
Die geglätteten Daten sind entweder die Summe der Niveaukomponente und der Saisonkomponente (additives Modell) oder das Produkt der Niveaukomponente und der Saisonkomponente (multiplikatives Modell).
Prognostizieren
Die prognostizierten Werte werden auch als Anpassungen bezeichnet. Bei den prognostizierten Werten handelt es sich um Punktschätzungen der Variablen zum Zeitpunkt (t).
Beobachtungen, bei denen die prognostizierten Werte stark von den beobachteten Werten abweichen, sind möglicherweise ungewöhnlich oder üben einen starken Einfluss aus. Versuchen Sie, die Ursache für alle Ausreißer zu identifizieren. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
Fehler
Die Fehlerwerte werden auch als Residuen bezeichnet. Die Fehlerwerte sind die Differenzen zwischen den beobachteten Werten und den prognostizierten Werten.
Interpretation
Stellen Sie die Fehlerwerte grafisch dar, um zu ermitteln, ob Ihr Modell angemessen ist. Die Werte können nützliche Informationen darüber liefern, wie gut das Modell an die Daten angepasst ist. Im Allgemeinen sollten die Fehlerwerte zufällig um 0 verteilt sein und weder offensichtliche Muster noch ungewöhnliche Werte aufweisen.
Periode
Wenn Sie Prognosen erstellen, zeigt Minitab die Periode an. Die Periode ist die Zeiteinheit der Prognose. Standardmäßig beginnt die Prognose am Ende der Daten.
Prognose
Bei den Prognosen handelt es sich um die angepassten Werte, die aus dem Zeitreihenmodell gewonnen werden. Minitab gibt die von Ihnen angegebene Anzahl von Prognosen aus. Die Prognosen beginnen entweder am Ende der Daten oder an dem von Ihnen angegebenen Ursprungspunkt.
Interpretation
Mit Prognosen können Sie eine Variable für einen bestimmten Zeitraum prognostizieren. Zum Beispiel kann eine Lagerverwalterin basierend auf den Bestellaktivitäten der letzten 60 Monate modellieren, wie viele Produkte sie in den nächsten drei Monaten bestellen muss.
Untersuchen Sie die Anpassungen und Prognosen im Diagramm, um zu ermitteln, wie genau die Prognosen sind. Die Anpassungen sollten eng an den Daten liegen, insbesondere am Ende der Datenreihe. Wenn Sie ein saisonales Modell verwenden, ist es besonders wichtig zu überprüfen, dass die Anpassungen am Ende der Zeitreihe den tatsächlichen Werten entsprechen. Falls das saisonale Muster oder der Trend nicht den Anpassungen am Ende der Datenreihe entspricht, sind die Prognosen wahrscheinlich weniger genau. Erfassen Sie in diesem Fall mehr Daten, damit das Modell die Änderungen im saisonalen Muster oder im Trend berücksichtigen kann.
Wenn das Modell am Ende der Datenreihe an das Modell angepasst ist, können Sie in der Regel mindestens einen vollständigen saisonalen Zyklus sicher voraussagen.
Untere und Obere
Die obere und die untere Prognosegrenze bilden ein Prognoseintervall für jede Prognose. Das Prognoseintervall stellt einen Bereich wahrscheinlicher Prognosewerte dar. Bei einem Prognoseintervall von 95 % können Sie sich z. B. zu 95 % sicher sein, dass das Prognoseintervall die Prognose zu dem angegebenen Zeitpunkt enthält.
Diagramm für die Winters-Methode
Das Diagramm stellt die Beobachtungen im Vergleich mit der Zeit dar. Das Diagramm enthält die mit dem Glättungsverfahren berechneten Anpassungen, die Prognosen, die Glättungskonstante und die Genauigkeitsmaße. Sie können auch festlegen, dass anstelle der Anpassungen die geglätteten Werte angezeigt werden.
Interpretation
- Wenn das Modell an Ihre Daten angepasst ist, können Sie Zerlegung ausführen und die beiden Modelle vergleichen.
- Wenn das Modell nicht an die Daten angepasst ist, untersuchen Sie das Diagramm auf das Fehlen von Saisonabhängigkeit. Wenn kein saisonales Muster vorliegt, sollten Sie eine andere Zeitreihenanalyse verwenden. Weitere Informationen finden Sie unter Welche Zeitreihenanalyse sollte verwendet werden?.
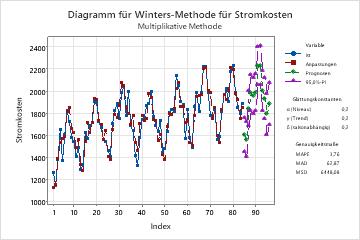
In diesem Diagramm liegen die Anpassungen eng an den Daten, was darauf hinweist, dass das Modell an Ihre Daten angepasst ist.
Histogramm der Residuen
Das Histogramm der Residuen zeigt die Verteilung der Residuen für alle Beobachtungen. Wenn das Modell gut an die Daten angepasst ist, sollten die Residuen zufällig ausfallen und den Mittelwert 0 aufweisen. Das Histogramm sollte also annähernd symmetrisch um 0 sein.
Wahrscheinlichkeitsnetz (Normal) für Residuen
Das Wahrscheinlichkeitsnetz (Normal) für Residuen stellt die Residuen im Vergleich zu den Werten dar, die bei Vorliegen einer Normalverteilung erwartet würden.
Interpretation
Prüfen Sie mit Hilfe des Wahrscheinlichkeitsnetzes (Normal) für Residuen, ob die Residuen normalverteilt sind. Für diese Analyse sind jedoch keine normalverteilten Residuen erforderlich.
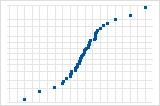
Die S-Kurve deutet auf eine Verteilung mit langen Randbereichen hin.
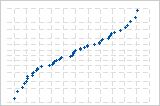
Die invertierte S-Kurve deutet auf eine Verteilung mit kurzen Randbereichen hin.
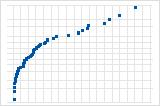
Eine Abwärtskurve deutet auf eine rechtsschiefe Verteilung hin.
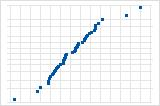
Wenige Punkte, die abseits der Linie liegen, deuten auf eine Verteilung mit Ausreißern hin.
Residuen vs. Anpassungen
Im Diagramm der Residuen im Vergleich mit den Anpassungen werden die Residuen auf der y-Achse und die angepassten Werte auf der x-Achse abgetragen.
Interpretation
Ermitteln Sie anhand des Diagramms „Residuen vs. Anpassungen“, ob die Residuen unverzerrt sind und eine konstante Varianz aufweisen. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte | Nicht konstante Varianz |
| Krümmung | Ein fehlender Term höherer Ordnung |
| Ein weit von null entfernt liegender Punkt | Ein Ausreißer |
Wenn Sie in den Residuen eine nicht konstante Varianz oder Muster erkennen, ist Ihre Prognose möglicherweise nicht genau.
Residuen vs. Reihenfolge
Das Diagramm der Residuen vs. Reihenfolge zeigt die Residuen in der Reihenfolge an, in der die Daten erfasst wurden.
Interpretation
Ermitteln Sie anhand des Diagramms der Residuen vs. Reihenfolge, wie genau die angepassten Werte im Vergleich zu den im Beobachtungszeitraum beobachteten Werten sind. Muster in den Punkten können darauf hinweisen, dass das Modell nicht an die Daten angepasst ist. Im Idealfall sollten die Residuen im Diagramm zufällig um die Mittellinie angeordnet sein.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Ein einheitlicher Langfrist-Trend | Das Modell ist nicht an die Daten angepasst. |
| Ein Kurzfrist-Trend | Eine Verschiebung oder Änderung im Muster |
| Ein weit von den anderen Punkten entfernt liegender Punkt | Ein Ausreißer |
| Ein Sprung in den Punkten | Das zugrunde liegende Muster der Daten hat sich geändert. |
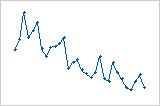
Die Residuen nehmen systematisch mit den von links nach rechts zunehmenden Beobachtungen ab.
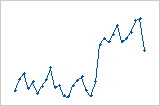
Es tritt eine sprunghafte Änderung in den Werten der Residuen von klein (links) nach groß (rechts) auf.
Residuen vs. Variablen
Das Diagramm der Residuen vs. Variablen zeigt die Residuen im Vergleich mit einer anderen Variablen.
Interpretation
Mit diesem Diagramm können Sie ermitteln, ob sich die Variable systematisch auf die Antwortvariable auswirkt. Wenn in den Residuen Muster vorhanden sind, besteht eine Assoziation zwischen den anderen Variablen und der Antwortvariablen. Sie können diese Informationen als Grundlage für weitere Untersuchungen verwenden.
