In diesem Thema
Eingeben der Daten
Geben Sie im Feld Variable eine Spalte mit numerischen Daten ein, die in regelmäßigen Intervallen erfasst und in zeitlicher Reihenfolge aufgezeichnet wurden. Wenn sich die Daten in mehreren Spalten befinden (z. B. die Daten für jedes Jahr in einer separaten Spalte), müssen Sie die Daten in einer einzigen Spalte stapeln.
In diesem Arbeitsblatt enthält die Spalte Verkäufe die Anzahl der Computer, die jeden Monat verkauft werden.
| C1 |
|---|
| Verkäufe |
| 195000 |
| 213330 |
| 208005 |
| 249000 |
| 237040 |
Modelltyp
- Stellen Sie die Daten mit Zeitreihendiagramm grafisch dar. Vergleichen Sie Ihr Diagramm dann mit den folgenden Abbildungen, um den korrekten Modelltyp zu ermitteln.
- Sie können die vier Modelle anpassen und die Genauigkeitsmaße (MAPE, MAD und MSD) vergleichen. Wählen Sie das Modell mit den kleinsten Genauigkeitsmaßen aus.
- Linear
-
Die Daten folgen einer Linie, was darauf hinweist, dass die Änderungsrate über die Zeit gleichmäßig ist. Das Modell lautet Yt = β0 + (β1 * t) + et. In diesem Modell stellt β1 die durchschnittliche Änderung von einer Periode zur nächsten dar.

- Quadratisch
-
Die Daten weisen eine Krümmung auf, was darauf hinweist, dass sich die Änderungsrate über die Zeit ändert. Das Modell lautet Yt = β0+ β1 * t + (β2* t2) + et.

- Exponentielles Wachstum
-
Die Daten weisen eine steile Krümmung auf, was darauf hinweist, dass sich die Änderungsrate über die Zeit immer schneller ändert. Beispielsweise kann ein Sparkonto ein exponentielles Wachstum aufweisen. Das Modell lautet Yt = β0 * β1t * et.
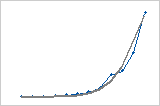
- S-Kurve (logistisches Pearl-Read-Modell)
-
Die Daten weisen eine S-Form auf, was darauf hinweist, dass sich die Richtung der Änderung mit der Zeit ändert. Das Modell lautet Yt = (10a) / (β0 + β1 * β2t).

Prognosen erstellen
Führen Sie die folgenden Schritte aus, um Prognosen für Ihre Zeitreihe zu erstellen.
- Wählen Sie Prognosen erstellen aus.
- Geben Sie im Feld Anzahl der Prognosen die Anzahl der aufeinander folgenden Perioden ein, für die Sie Prognosen erstellen möchten.
- Geben Sie im Feld Start bei
Ausgangswert die Zeilennummer für die erste Prognose an. Wenn Sie dieses Feld leer lassen, beginnt Minitab mit den Prognosen am Ende der Zeitreihe.
Wenn Sie einen Wert eingeben, verwendet Minitab für die Prognosen nur die Daten bis zu dieser Zeilennummer. Die Prognosewerte weichen von den Anpassungen ab, weil Minitab für die Berechnung der Anpassungen alle Daten verwendet.
Einem Analytiker liegen beispielsweise monatliche Daten von Januar bis Dezember vor. Im Dezember möchte der Analytiker eine Prognose für den nächsten Monat erstellen, die Daten von Dezember sind jedoch unvollständig. Der Analytiker gibt im Feld Anzahl der Prognosen den Wert 2 und im Feld Start bei Ausgangswert den Wert 12 ein. Minitab verwendet die Daten bis November, um Prognosen für Dezember und Januar zu erstellen.
