Methoden und Formeln für Trendanalyse

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Linear
Exponentielles Wachstum
Quadratisch
S-Kurve
Gewichtungen
Prognosen
MAPE
MAD
MSD

Linear

Formel

Das lineare Trendmodell lautet folgendermaßen:

Y_t = β₀ + β₁ t + e_t

Notation

Begriff	Beschreibung
β₀	Konstante
β₁	durchschnittliche Änderung zwischen einer Periode und der nächsten
t	Wert der Zeiteinheit
e_t	Fehlerterm

Exponentielles Wachstum

Formel

Das Trendmodell für exponentielles Wachstum kann exponentielles Wachstum oder exponentielle Rückgänge erklären. Beispielsweise kann ein Sparkonto ein exponentielles Wachstum aufweisen.

Y_t = β₀ * β₁^t * e_t

Notation

Begriff	Beschreibung
β₀	Konstante
β₁	Koeffizient
t	Wert der Zeiteinheit
e_t	Fehlerterm

Quadratisch

Formel

Das quadratische Trendmodell kann einfache Krümmungen in den Daten erklären und lautet folgendermaßen:

Y_t = β₀ + β₁ t + β₂ t² + e_t

Notation

Begriff	Beschreibung
β₀	Konstante
β₁ und β₂	Koeffizienten
t	Wert der Zeiteinheit
e_t	Fehlerterm

S-Kurve

Formel

Die Daten weisen eine S-Form auf, was darauf hinweist, dass sich die Richtung der Änderung mit der Zeit ändert.

Y_t = 10^a / (β₀ + β₁ β₂^t)

Notation

Begriff	Beschreibung
β₀	Konstante
β₁ und β₂	Koeffizienten
t	Wert der Zeiteinheit

Gewichtungen

Wenn Sie Koeffizienten aus einer früheren Anpassung einer Trendanalyse bereitstellen, führt Minitab eine gewichtete Trendanalyse durch. Wenn die Gewichtung eines bestimmten Koeffizienten α ist, wird der neue Koeffizient in Minitab wie folgt geschätzt:

Formel

α p₁ + (1 – α)p₂

Notation

Begriff	Beschreibung
p₁	aus den aktuellen Daten geschätzter Koeffizient
p₂	vorheriger Koeffizient

Prognosen

Minitab verwendet die Trendgleichung, um die Prognosen für bestimmte Zeitwerte zu berechnen. Für die Anpassung des Trends werden die Daten vor dem Prognoseursprung verwendet.

MAPE

Der mittlere absolute prozentuale Fehler (MAPE) ist eine Maßzahl für die Genauigkeit der angepassten Zeitreihenwerte. MAPE drückt die Genauigkeit als Prozentsatz aus.

Formel

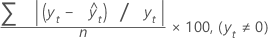
Notation

Begriff	Beschreibung
y_t	tatsächlicher Wert zum Zeitpunkt t
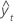	angepasster Wert
n	Anzahl der Beobachtungen

MAD

Die mittlere absolute Abweichung (MAD) ist eine Maßzahl für die Genauigkeit der angepassten Zeitreihenwerte. MAD drückt die Genauigkeit in der gleichen Einheit wie die Daten aus, wodurch der Fehlerbetrag leichter erfasst werden kann.

Formel

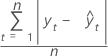
Notation

Begriff	Beschreibung
y_t	tatsächlicher Wert zum Zeitpunkt t
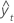	angepasster Wert
n	Anzahl der Beobachtungen

MSD

Die mittlere quadrierte Abweichung (MSD) wird immer mit demselben Nenner n berechnet, unabhängig vom Modell. MSD ist bei ungewöhnlich großen Prognosefehlern ein empfindlicheres Maß als MAD.

Formel

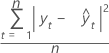
Notation

Begriff	Beschreibung
y_t	tatsächlicher Wert zum Zeitpunkt t
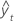	angepasster Wert
n	Anzahl der Beobachtungen