Methoden und Formeln für Einfache exponentielle Glättung

Die geglätteten Werte werden auf eine von zwei Arten erhalten: mit einem optimalen Gewicht, das von Minitab erzeugt wird, oder einem von Ihnen angegebenen Gewicht.

Optimale ARIMA-Gewichtung

1. Minitab passt zu einem ARIMA-Modell (0,1,1) ohne Konstante und speichert die Fitts.
2. Der anfängliche geglättete Wert der Single Exponential Smoothing-Analyse ist die erste nicht fehlende Passung aus dem ARIMA-Modell.
3. Da die Anpassungen eine verzögerte Eingangseinheit sind, verwendet Minitab Backcasting, um den initialen angepassten Wert (zum Zeitpunkt eins) zu berechnen:
   • Initial angepasster Wert = [Der erste geglättete Wert – α (erster Datenwert)] / (1 – α)

Notation

Angegebene Gewichtung

1. Minitab verwendet für den anfänglichen geglätteten Wert (zum Zeitpunkt null) den Durchschnitt der ersten sechs (oder N, wenn N < 6) Beobachtungen. Analog dazu verwendet Minitab den Durchschnitt der ersten sechs (oder N, wenn N < 6) Beobachtungen für den anfänglichen angepassten Wert (zum Zeitpunkt eins). Anpassung(i) = geglätteter Wert(i – 1).
2. Die folgenden geglätteten Werte werden aus der Formel berechnet:
   • Glätteter Wert zum Zeitpunkt t = α (Daten bei t) + (1 – α) (geglätteter Wert zum Zeitpunkt t – 1)

Notation

Der angepasste Wert zum Zeitpunkt t stellt den geglätteten Wert zum Zeitpunkt t – 1 dar. Bei den Prognosen handelt es sich um die angepassten Werte am Prognoseursprung. Wenn Sie eine Prognose für 10 Zeiteinheiten in der Zukunft erstellen, ist der prognostizierte Wert zu jedem Zeitpunkt der angepasste Wert am Ursprung. Für die Glättung werden die Daten bis zum Prognoseursprung verwendet.

Bei der naiven Prognose ist die Prognose für Zeitpunkt t der Datenwert zum Zeitpunkt t – 1. Führen Sie für eine naive Prognose eine einfache exponentielle Glättung mit der Gewichtung eins aus.

Formel

Der Wert 1,25 ist eine angenäherte Konstante für die Proportionalität zwischen der Standardabweichung und der mittleren absoluten Abweichung. 1,25 × MAD entspricht also etwa der Standardabweichung.

Der mittlere absolute prozentuale Fehler (MAPE) ist eine Maßzahl für die Genauigkeit der angepassten Zeitreihenwerte. MAPE drückt die Genauigkeit als Prozentsatz aus.

Formel

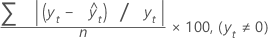
Notation

Begriff	Beschreibung
yt	tatsächlicher Wert zum Zeitpunkt t
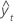	angepasster Wert
n	Anzahl der Beobachtungen

Die mittlere absolute Abweichung (MAD) ist eine Maßzahl für die Genauigkeit der angepassten Zeitreihenwerte. MAD drückt die Genauigkeit in der gleichen Einheit wie die Daten aus, wodurch der Fehlerbetrag leichter erfasst werden kann.

Formel

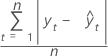
Notation

Begriff	Beschreibung
yt	tatsächlicher Wert zum Zeitpunkt t
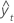	angepasster Wert
n	Anzahl der Beobachtungen

Die mittlere quadrierte Abweichung (MSD) wird immer mit demselben Nenner n berechnet, unabhängig vom Modell. MSD ist bei ungewöhnlich großen Prognosefehlern ein empfindlicheres Maß als MAD.

Formel

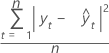
Notation

Begriff	Beschreibung
yt	tatsächlicher Wert zum Zeitpunkt t
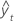	angepasster Wert
n	Anzahl der Beobachtungen