Methoden und Formeln für Gleitender Durchschnitt (MA)

Um einen gleitenden Durchschnitt zu berechnen, mittelt Minitab aufeinander folgende Gruppen von Beobachtungen in einer Datenreihe. Angenommen, eine Datenreihe beginnt mit den Zahlen 4, 5, 8, 9, 10, und Sie verwenden eine Länge des gleitenden Durchschnitts von 3. Die ersten zwei Werte des gleitenden Durchschnitts fehlen. Der dritte gleitende Durchschnitt ist der Durchschnitt von 4, 5, 8; der vierte Wert ist der Durchschnitt von 5, 8, 9; der fünfte Wert ist der Durchschnitt von 8, 9, 10.

In der Standardeinstellung werden Werte der gleitenden Durchschnitte in der Periode angeordnet, in der sie berechnet wurden. Bei einer Länge des gleitenden Durchschnitts von 3 wird beispielsweise der erste numerische Wert des gleitenden Durchschnitts in der Periode 3 angeordnet, der nächste in der Periode 4 usw.

Wenn Sie gleitende Durchschnitte zentrieren, werden diese im Zentrum der Spannweite anstatt an deren Ende angeordnet. Dies wird durchgeführt, damit die Werte der gleitenden Durchschnitte in deren zentralen Positionen im Zeitverlauf angeordnet werden.

Länge des gleitenden Durchschnitts ist ungerade

Angenommen, die Länge des gleitenden Durchschnitts beträgt 3. In diesem Fall ordnet Minitab den ersten numerischen Wert des gleitenden Durchschnitts in Periode 2, den nächsten in Periode 3 usw. an. In diesem Fall fehlt der Wert (*) des gleitenden Durchschnitts für die erste und letzte Periode.

Länge des gleitenden Durchschnitts ist gerade

Angenommen, die Länge des gleitenden Durchschnitts beträgt 4. Da Sie einen Wert des gleitenden Durchschnitts nicht in Periode 2,5 anordnen können, berechnet Minitab den Durchschnittswert der ersten vier Werte und bezeichnet diesen als GD1. Dann berechnet Minitab den Durchschnitt der nächsten vier Werte und bezeichnet diesen als GD2. Den Durchschnitt dieser beiden Werte ordnet Minitab in Periode 3 an. In diesem Fall sind die Werte der gleitenden Durchschnitte in den ersten zwei und den letzten zwei Perioden fehlende Werte (*).

Der angepasste Wert zum Zeitpunkt t stellt den nicht zentrierten gleitenden Durchschnitt zum Zeitpunkt t–1 dar. Bei den Prognosen handelt es sich um die angepassten Werte am Prognoseursprung. Wenn Sie eine Prognose für 10 Zeiteinheiten in der Zukunft erstellen, ist der prognostizierte Wert zu jedem Zeitpunkt der angepasste Wert am Ursprung. Zum Berechnen der gleitenden Durchschnitte werden die Daten bis zum Ursprung verwendet.

Sie können die Methode der linearen gleitenden Durchschnitte verwenden, um aufeinander folgende gleitende Durchschnitte zu berechnen. Dies wird häufig vorgenommen, wenn die Daten einen Trend aufweisen. Berechnen und speichern Sie zuerst den gleitenden Durchschnitt der ursprünglichen Zeitreihe. Berechnen und speichern Sie anschließend den gleitenden Durchschnitt der zuvor gespeicherten Spalte, um einen zweiten gleitenden Durchschnitt zu erhalten.

In naiven Prognosen ist die Prognose für den Zeitpunkt t der Datenwert zum Zeitpunkt t–1. Wenn Sie das Verfahren des gleitenden Durchschnitts mit einem gleitenden Durchschnitt der Länge 1 durchführen, erhalten Sie eine naive Prognose.

Formel

Obergrenze = Prognose + 1,96 ×

Untergrenze = Prognose - 1,96 ×

Notation

Der mittlere absolute prozentuale Fehler (MAPE) ist eine Maßzahl für die Genauigkeit der angepassten Zeitreihenwerte. MAPE drückt die Genauigkeit als Prozentsatz aus.

Formel

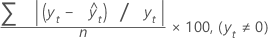
Notation

Begriff	Beschreibung
yt	tatsächlicher Wert zum Zeitpunkt t
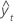	angepasster Wert
n	Anzahl der Beobachtungen

Die mittlere absolute Abweichung (MAD) ist eine Maßzahl für die Genauigkeit der angepassten Zeitreihenwerte. MAD drückt die Genauigkeit in der gleichen Einheit wie die Daten aus, wodurch der Fehlerbetrag leichter erfasst werden kann.

Formel

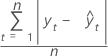
Notation

Begriff	Beschreibung
yt	tatsächlicher Wert zum Zeitpunkt t
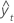	angepasster Wert
n	Anzahl der Beobachtungen

Die mittlere quadrierte Abweichung (MSD) wird immer mit demselben Nenner n berechnet, unabhängig vom Modell. MSD ist bei ungewöhnlich großen Prognosefehlern ein empfindlicheres Maß als MAD.

Formel

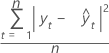
Notation

Begriff	Beschreibung
yt	tatsächlicher Wert zum Zeitpunkt t
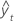	angepasster Wert
n	Anzahl der Beobachtungen