Führen Sie die entsprechenden Schritte für die Modelle aus, die Sie auswerten möchten. Die Schritte sind für saisonale und nicht-saisonale Modelle gleich, aber die Details unterscheiden sich.
Passen Sie ein nicht saisonales ARIMA-Modell an
Führen Sie die folgenden Schritte aus, um die Spalten mit den zu analysierenden Daten anzugeben- Mit nicht Saisonkomponente ARIMA-Modell. Wenn Sie Modelle mit einem konstanten Term anpassen, haben Kandidatenmodelle p + q ≤ 9. Wenn Sie Modelle ohne konstanten Begriff anpassen, haben Kandidatenmodelle p + q ≤ 10. Kandidatenmodelle mit d = 2 sind ohne konstanten Term fit.
Voraussetzungen
In der Regel bewerten Sie den Bedarf an einer Transformation und bestimmen die abweichende Reihenfolge, bevor Sie mit dieser Analyse beginnen.
Transformation
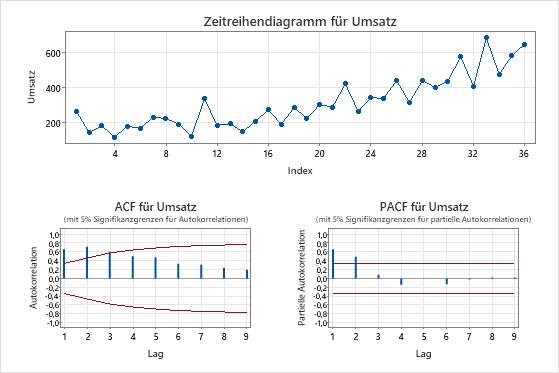
Verwenden Sie ein Zeitreihendiagramm, um zu bestimmen, ob die Varianz einer Zeitreihe stationär ist. Wenn die Zeitreihe ein Muster in der Streuung der Punkte aufweist, ist die Varianz nicht stationär. Verwenden Sie eine Box-Cox-Transformation einer Zeitreihe, um zu versuchen, die Varianz der Reihe stationär zu machen. Um eine Box-Cox-Transformation für eine Zeitreihe auszuwerten, wählen Sie . Statistik > Zeitreihen > Box-Cox-Transformation Informationen zur Verwendung einer Box-Cox-Transformation in Prognose mit
bestem
ARIMA-Modellfinden Sie unter Auswählen der Analyseoptionen für Prognose mit bestem ARIMA-Modell.
Differenzierende Reihenfolge
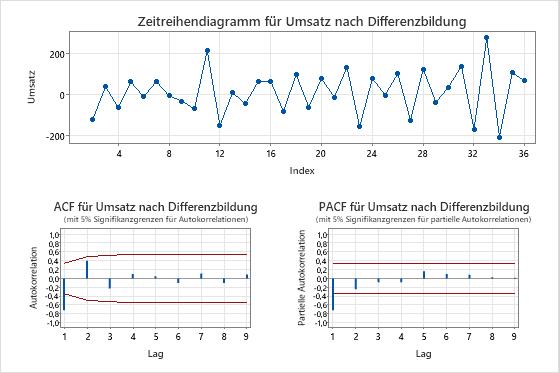
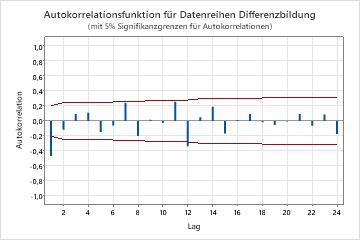
Untersuchen Sie ein Diagramm der Autokorrelationsfunktion (ACF) für eine Reihe, um die Reihenfolge der Differenzierung zu bestimmen. Das übliche Muster auf einem ACF-Diagramm, das die Notwendigkeit einer Differenzierung zeigt, ist ein Trend, der langsam abnimmt. Wenn die Daten eine weitere Differenzierung unterstützen, tritt das gleiche Muster in der ACF der differenzierten Daten auf. Um eine Autokorrelationsanalyse durchzuführen, wählen Sie Statistik > Zeitreihen > Autokorrelation aus. Berücksichtigen Sie auch den erweiterten Dickey-Fuller-Test , um die Reihenfolge zu bestimmen. Geben Sie die Differenzierungsreihenfolge an, wenn Sie die Modelle auswerten.
ACF-Diagramm einer Zeitreihe mit einem Trend
In diesen Ergebnissen zeigt das Zeitreihendiagramm der Originaldaten einen klaren Trend. Das Zeitreihendiagramm der differenzierten Daten zeigt die Unterschiede zwischen aufeinanderfolgenden Werten. Die differenzierten Daten erscheinen stationär, da die Punkte einem horizontalen Pfad ohne offensichtliche Muster in der Variation folgen.
Die ACF-Diagramme zeigen auch den Effekt der Differenzierung. In diesen Ergebnissen zeigt das ACF-Diagramm der Originaldaten langsam verringerte Spitzen über Lags hinweg. Dieses Muster zeigt an, dass die Daten nicht stationär sind. Im ACF-Diagramm der differenzierten Daten befindet sich die einzige Spitze, die sich signifikant von 0 unterscheidet, bei Verzögerung 1.
Evaluierung nicht saisonaler Modelle
Geben Sie im Feld Datenreihe eine Spalte mit numerischen Daten ein, die in regelmäßigen Intervallen erfasst und in zeitlicher Reihenfolge aufgezeichnet wurden.
Wählen Sie unter Ordnung für Differenzbildung ddie Reihenfolge für die nicht saisonale Differenzierung aus.
Wählen Sie für Ordnung für Autoregression peinen Minimalwert für die Auswertung und einen Maximalwert für die Auswertung aus. Die Analyse passt Modelle mit allen Kombinationen von autoregressiven und gleitenden Durchschnittsordnungen in den Auswahlmöglichkeiten an. Wenn Sie für das Minimum und das Maximum denselben Wert eingeben, verwendet die Analyse diesen Wert für alle Kandidatenmodelle.
Wählen Sie für Ordnung für gleitenden Durchschnitt qeinen Minimalwert für die Auswertung und einen Maximalwert für die Auswertung aus. Die Analyse passt Modelle mit allen Kombinationen von autoregressiven und gleitenden Durchschnittsordnungen in den Auswahlmöglichkeiten an. Wenn Sie für das Minimum und das Maximum denselben Wert eingeben, verwendet die Analyse diesen Wert für alle Kandidatenmodelle.
Aktivieren Konstanten Term in Modelle einbinden, um den konstanten Term in das Regressionsmodell einzubinden. Mit einem konstanten Term kann das Modell eine Reihe schätzen, bei der der Mittelwert nicht 0 ist. Ohne einen konstanten Term ist der Mittelwert der Reihe, in die das Modell passt, 0. Wenn die Analyse ein Modell nicht mit einem konstanten Term anpassen kann, versucht die Analyse, das Modell ohne den konstanten Term anzupassen.
Geben Sie im Feld Anzahl der Prognosen die Anzahl der aufeinander folgenden Perioden ein, für die Sie Prognosen erstellen möchten. Normalerweise geben Sie die Mindestanzahl ein, um die gewünschte Prognose bereitzustellen. Wenn Sie beispielsweise über monatliche Daten verfügen und eine Prognose für 6 Monate nach dem Ende der Datenreihe erhalten möchten, geben Sie 6ein.
Wählen Sie Prognose ab dem Ende der Datenreihe oder Prognose ab dem k-ten Wert in der Datenreihe aus. Wenn Sie einen Wert eingeben, verwendet Minitab für die Prognosen nur die Daten bis zu dieser Zeilennummer. Die Prognosewerte weichen von den Anpassungen ab, weil Minitab für die Berechnung der Anpassungen alle Daten verwendet. Einem Analytiker liegen beispielsweise monatliche Daten für 5 Jahre jeweils von Januar bis Dezember vor. Der Analytiker möchte eine Prognose für den nächsten Monat erstellen, aber die Daten des letzten Monats Dezember sind unvollständig. Der Analyst gibt die Prognose ab dem 59. Wert in der Reihe an und gibt zwei Prognosen an. die Analyse verwendet die Daten der ersten 59 Monate, um eine Prognose für Dezember und Januar zu erstellen.
Bevor Sie ein ARIMA-Modell für die Prognose verwenden, stellen Sie sicher, dass das Modell gut zu den Daten passt. Untersuchen Sie die Restdiagnose, um festzustellen, ob das Modell die Annahmen für ein ARIMA-Modell erfüllt. Weitere Informationen finden Sie unter Interpretieren der wichtigsten Ergebnisse für Prognose mit bestem ARIMA-Modell.
Passen Sie ein saisonales ARIMA Modell an
Führen Sie die folgenden Schritte aus, um die Spalten mit den zu analysierenden Daten anzugeben- Mit Saisonkomponente ARIMA-Modell. Wenn Sie Modelle mit einem konstanten Term anpassen, haben Kandidatenmodelle p + q + P + Q ≤ 9. Wenn Sie Modelle ohne konstanten Term anpassen, haben Kandidatenmodelle p + q + P + Q ≤ 10. Kandidatenmodelle mit d + D > 1 sind ohne konstante Laufzeit geeignet.
Voraussetzungen
In der Regel bewerten Sie den Bedarf an einer Transformation und bestimmen die abweichende Reihenfolge, bevor Sie mit dieser Analyse beginnen.
Transformation
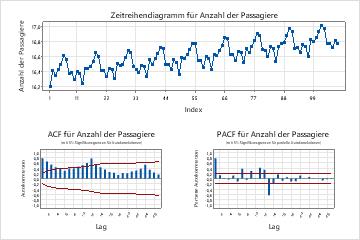
Verwenden Sie ein Zeitreihendiagramm, um zu bestimmen, ob die Varianz einer Zeitreihe stationär ist. Wenn die Zeitreihe ein Muster in der Streuung der Punkte aufweist, ist die Varianz nicht stationär. Verwenden Sie eine Box-Cox-Transformation einer Zeitreihe, um zu versuchen, die Varianz der Reihe stationär zu machen. Um eine Box-Cox-Transformation für eine Zeitreihe auszuwerten, wählen Sie . Statistik > Zeitreihen > Box-Cox-Transformation Informationen zur Verwendung einer Box-Cox-Transformation in Prognose mit
bestem
ARIMA-Modellfinden Sie unter Auswählen der Analyseoptionen für Prognose mit bestem ARIMA-Modell.
Differenzierende Reihenfolge
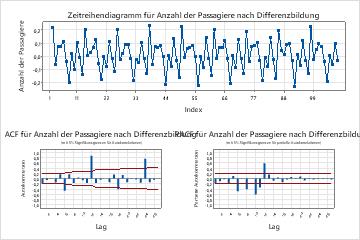
Untersuchen Sie ein Diagramm der Autokorrelationsfunktion (ACF) für eine Reihe, um die nicht saisonalen und saisonalen Ordnungen der Differenzierung zu bestimmen. Ein saisonales Muster, das sich jede k-te Periode wiederholt, bedeutet, dass Sie die k-te Differenz berechnen sollten, um einen Teil des Musters zu entfernen. Ein Trend, der langsam abnimmt, deutet darauf hin, dass Sie auch einen nicht-saisonalen Unterschied verwenden sollten. Wenn die Daten eine weitere Differenzierung unterstützen, treten die gleichen Muster in der ACF der differenzierten Daten auf. Größenordnungen mit saisonalen Unterschieden größer als 1 sind selten. Um eine Autokorrelationsanalyse durchzuführen, wählen Sie Statistik > Zeitreihen > Autokorrelation aus. Geben Sie beim Auswerten der Modelle differenzierende Reihenfolgen an.
ACF-Diagramm einer Zeitreihe mit einem Trend und einem saisonalen Muster
In diesen Ergebnissen zeigt das Zeitreihendiagramm der Originaldaten einen Aufwärtstrend und ein saisonales Muster mit einem Zeitraum von 12. Das Zeitreihendiagramm der differenzierten Daten zeigt die Unterschiede zwischen aufeinanderfolgenden Werten.
Das ACF-Diagramm für die Daten nach der Differenzierung zeigt die Auswirkungen der nicht saisonalen Differenzierung. In diesen Ergebnissen zeigt das ACF-Diagramm der Originaldaten langsam verringerte Spitzen über Lags hinweg. Spikes erscheinen auch bei den saisonalen Lags. Diese 2 Muster zeigen an, dass die Daten nicht stationär sind. Im ACF-Diagramm der Daten nach nicht-saisonalen Differenzierungen liegen die signifikanten Spitzen bei den saisonalen Verzögerungen.
Das ACF-Diagramm der Daten nach einer saisonalen Differenz und einer nicht saisonalen Differenz zeigt nicht das saisonale Muster. Die für diese Daten geeigneten Differenzierungsreihenfolgen sind 1 nicht saisonale Differenz und 1 saisonale Differenz.
Evaluierung saisonaler Modelle
Geben Sie im Feld Datenreihe eine Spalte mit numerischen Daten ein, die in regelmäßigen Intervallen erfasst und in zeitlicher Reihenfolge aufgezeichnet wurden.
Wählen Sie unter Ordnung für Differenzbildung ddie Reihenfolge für die nicht saisonale Differenzierung aus.
Wählen Sie für Ordnung für Autoregression peinen Minimalwert für die Auswertung und einen Maximalwert für die Auswertung aus. Die Analyse passt Modelle mit allen Kombinationen von autoregressiven und gleitenden Durchschnittsordnungen in den Auswahlmöglichkeiten an. Wenn Sie für das Minimum und das Maximum denselben Wert eingeben, verwendet die Analyse diesen Wert für alle Kandidatenmodelle.
Wählen Sie für Ordnung für gleitenden Durchschnitt qeinen Minimalwert für die Auswertung und einen Maximalwert für die Auswertung aus. Die Analyse passt Modelle mit allen Kombinationen von autoregressiven und gleitenden Durchschnittsordnungen in den Auswahlmöglichkeiten an. Wenn Sie für das Minimum und das Maximum denselben Wert eingeben, verwendet die Analyse diesen Wert für alle Kandidatenmodelle.
Geben Sie im Feld Modelle mit Saisonkomponente anpassen mit Periode die Länge des saisonalen Musters ein. Wenn Sie die Daten z. B. monatlich erfassen und die Daten ein jährliches Muster aufweisen, geben Sie 12 ein.
Wählen Sie unter Ordnung für Differenzbildung mit Saisonkomponente Ddie Reihenfolge für die saisonale Differenzierung aus. Die meisten Reihen mit einem saisonalen Muster verwenden eine saisonale Reihenfolge der Differenzierung, um die Daten stationär zu machen. 1 ist für die meisten saisonalen Muster ausreichend.
Wählen Sie für Ordnung für Autoregression Peinen Minimalwert für die Auswertung und einen Maximalwert für die Auswertung aus. Die Analyse passt Modelle mit allen Kombinationen von autoregressiven und gleitenden Durchschnittsordnungen in den Auswahlmöglichkeiten an. Wenn Sie für das Minimum und das Maximum denselben Wert eingeben, verwendet die Analyse diesen Wert für alle Kandidatenmodelle.
Wählen Sie für Ordnung für gleitenden Durchschnitt Qeinen Minimalwert für die Auswertung und einen Maximalwert für die Auswertung aus. Die Analyse passt Modelle mit allen Kombinationen von autoregressiven und gleitenden Durchschnittsordnungen in den Auswahlmöglichkeiten an. Wenn Sie für das Minimum und das Maximum denselben Wert eingeben, verwendet die Analyse diesen Wert für alle Kandidatenmodelle.
Aktivieren Konstanten Term in Modelle einbinden, um den konstanten Term in das Regressionsmodell einzubinden. Mit einem konstanten Term kann das Modell eine Reihe schätzen, bei der der Mittelwert nicht 0 ist. Ohne einen konstanten Term ist der Mittelwert der Reihe, in die das Modell passt, 0. Wenn die Analyse ein Modell nicht mit einem konstanten Term anpassen kann, versucht die Analyse, das Modell ohne den konstanten Term anzupassen.
Geben Sie im Feld Anzahl der Prognosen die Anzahl der aufeinander folgenden Perioden ein, für die Sie Prognosen erstellen möchten. Normalerweise geben Sie die Mindestanzahl ein, um die gewünschte Prognose bereitzustellen. Wenn Sie beispielsweise über monatliche Daten verfügen und eine Prognose für 6 Monate nach dem Ende der Datenreihe erhalten möchten, geben Sie 6ein.
Wählen Sie Prognose ab dem Ende der Datenreihe oder Prognose ab dem k-ten Wert in der Datenreihe aus. Wenn Sie einen Wert eingeben, verwendet Minitab für die Prognosen nur die Daten bis zu dieser Zeilennummer. Die Prognosewerte weichen von den Anpassungen ab, weil Minitab für die Berechnung der Anpassungen alle Daten verwendet. Einem Analytiker liegen beispielsweise monatliche Daten für 5 Jahre jeweils von Januar bis Dezember vor. Der Analytiker möchte eine Prognose für den nächsten Monat erstellen, aber die Daten des letzten Monats Dezember sind unvollständig. Der Analyst gibt die Prognose ab dem 59. Wert in der Reihe an und gibt zwei Prognosen an. die Analyse verwendet die Daten der ersten 59 Monate, um eine Prognose für Dezember und Januar zu erstellen.
Bevor Sie ein ARIMA-Modell für die Prognose verwenden, stellen Sie sicher, dass das Modell gut zu den Daten passt. Untersuchen Sie die Restdiagnose, um festzustellen, ob das Modell die Annahmen für ein ARIMA-Modell erfüllt. Weitere Informationen finden Sie unter Interpretieren der wichtigsten Ergebnisse für Prognose mit bestem ARIMA-Modell.
