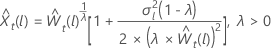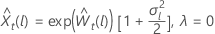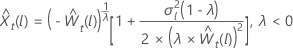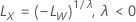Prognose mit bestem ARIMA-Modell Vergleicht viele Modelle und wählt ein endgültiges Modell mit einem Kriterium in den Spezifikationen der Analyse aus. Informationen zu den Ergebnissen des endgültigen ARIMA-Modells finden Sie unter Methoden und Formeln für ARIMA. Die folgenden Abschnitte enthalten Details, die für eindeutig sind. Prognose mit bestem ARIMA-Modell
Modellauswahl
Bei der Modellauswahl werden die folgenden Schritte ausgeführt:
- Schätzen Sie die Modellparameter für jedes Modell. Wenn ein Modell eine Konstante enthält und die Schätzung der Parameter fehlschlägt, versuchen Sie, die Parameter ohne den konstanten Term zu schätzen.
- Berechnen Sie das Informationskriterium für jedes Modell. Das Standardkriterium ist das korrigierte Akaike Information Criterion (AICc).
- Erzeugen Sie Ergebnisse für das Modell mit dem besten Wert des Informationskriteriums.
In den folgenden Abschnitten werden Details beschrieben, die sich bei der Auswahl von nicht saisonalen und saisonalen Modellen unterscheiden.
Nicht saisonales Modelle
- Wenn Sie Modelle mit einem konstanten Term anpassen, haben Kandidatenmodelle p + q ≤ 9.
- Wenn Sie Modelle ohne konstanten Begriff anpassen, haben Kandidatenmodelle p + q ≤ 10.
- Modelle mit d = 2 enthalten niemals einen konstanten Term.
- Das Modell wertet ARIMA(0, d, 0) nur aus, wenn d = 1 ist.
Saisonale Modelle
- Wenn Sie Modelle mit einem konstanten Term anpassen, haben Kandidatenmodelle p + q + P + Q ≤ 9.
- Wenn Sie Modelle ohne konstanten Term anpassen, haben Kandidatenmodelle p + q + P + Q ≤ 10.
- Modelle mit d + D > 1 enthalten niemals einen konstanten Begriff.
- Die Suche nach einem saisonalen Modell erfordert die Reihenfolge mindestens eines der saisonalen Parameter, um größer als 0 sein zu können. Die Suche umfasst nicht saisonale Modelle, wenn die Spezifikationen für die Suche Modelle enthalten, bei denen alle saisonalen Parameter Ordnungen von 0 haben.
- Mindestens 1 von p, q, P und Q ist in jedem Modell ungleich Null.
Kriterien
- Akaike Information Criterion (AIC)
- Akaikes korrigiertes Informationskriterium (AICc)
- Bayessche Informationskriterium (BIC)
Bei der Berechnung der Informationskriterien für ein Modell wird der Log-Likelihood-Wert für das Modell verwendet. Bei der Berechnung des Log-Likelihood-Werts wird ein rekursiver Algorithmus verwendet. Weitere Informationen finden Sie in Abschnitt 8.6 von Brockwell & Davis (1991)1.
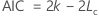
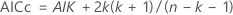

Notation
| Begriff | Beschreibung |
|---|---|
| k | Die Anzahl der Parameter im Modell
|
| Lc | Log-Likelihood des aktuellen Modells |
| n | Stichprobenumfang der Zeitreihe |
Box-Cox-Transformation
Die Analyse ermöglicht eine Box-Cox-Transformation der Daten. Die Transformation der Daten erfolgt vor der Modellauswahl. Informationen zur Box-Cox-Transformation für Zeitreihendaten finden Sie unter Methoden und Formeln für Box-Cox Transformation für Zeitreihen.
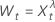 für λ > 0
für λ > 0 für λ = 0
für λ = 0 für λ < 0
für λ < 0
Dabei gilt: 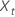 ist der t-te Wert der ursprünglichen Zeitreihe und t = 1, ..., n.
ist der t-te Wert der ursprünglichen Zeitreihe und t = 1, ..., n.
Sei 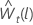 ist der l-te Prognosewert, beginnend mit dem Ursprung tfür die transformierten Daten. Sei
ist der l-te Prognosewert, beginnend mit dem Ursprung tfür die transformierten Daten. Sei  die L-Schritt-Prognoseabweichung von den transformierten Daten sein. Dann hängt der l-te Prognosewert von t für die ursprüngliche Reihe vom Wert von λab:
die L-Schritt-Prognoseabweichung von den transformierten Daten sein. Dann hängt der l-te Prognosewert von t für die ursprüngliche Reihe vom Wert von λab:
Dabei gilt:  ist der Grenzwert im ursprünglichen Maßstab und
ist der Grenzwert im ursprünglichen Maßstab und 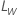 ist der Grenzwert in der transformierten Skala.
ist der Grenzwert in der transformierten Skala.
Zielloser Spaziergang Modell
Das ARIMA(0, 1, 0)-Modell, mit oder ohne konstanten Term, ist das Random-Walk-Modell. Passt in Minitab Statistical Software Prognose mit bestem ARIMA-Modell das Random-Walk-Modell an. Der Befehl erfordert mindestens einen autoregressiven oder gleitenden Durchschnittsparameter. Die Schätz- und Wahrscheinlichkeitsgrenzen für das Random-Walk-Modell haben spezifische Formen. Die Berechnungen für die Logwahrscheinlichkeit, die Prognosegrenzen und die Wahrscheinlichkeitsgrenzen für die Prognosen hängen davon ab, ob das Modell einen konstanten Term enthält.
Definitionen:
| Begriff | Beschreibung |
|---|---|
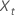 | die Beobachtungen für eine Zeitreihe mit t = 1, ..., n |
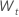 | die ersten differenzierten Daten aus der ursprünglichen Zeitreihe,  |
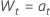
oder
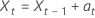
Dabei gilt: 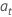 sind unabhängig und identisch verteilt und folgen der Normalverteilung mit Mittelwert 0 und Varianz σ2, t = 2, ..., n.
sind unabhängig und identisch verteilt und folgen der Normalverteilung mit Mittelwert 0 und Varianz σ2, t = 2, ..., n.
Gleichungen, die das Modell mit einer Konstanten darstellen, sind ähnlich:

oder
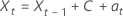

Modell ohne konstanten Term
Die Log-Wahrscheinlichkeit weist die folgende Form auf:
Log-Wahrscheinlichkeit
Dabei gilt Folgendes:
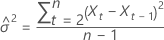

Die Wahrscheinlichkeitsgrenze von 100 × (1 – α) für den Prognosewert 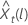 die folgende Form:
die folgende Form:
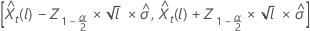
Dabei gilt:  steht für dar 100× 1– α/2)- d Perzentil aus der Standardnormalverteilung.
steht für dar 100× 1– α/2)- d Perzentil aus der Standardnormalverteilung.
Modell mit konstanten Term
Für ein Modell mit einer Konstanten erfordern die Berechnungen für die Loglikelihood die Schätzung der Konstante C. Unterscheiden Sie zunächst die Daten von der Originalserie 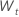 für t = 2, ..., n. Die Konstante ist der Stichprobenmittelwert von
für t = 2, ..., n. Die Konstante ist der Stichprobenmittelwert von 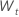 Hat die folgende Form:
Hat die folgende Form:
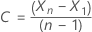
Die Log-Wahrscheinlichkeit weist die folgende Form auf:
Log-Wahrscheinlichkeit
Dabei gilt Folgendes:
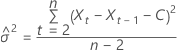
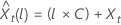
Die Wahrscheinlichkeitsgrenze von 100 × (1 – α) für den Prognosewert 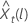 die folgende Form:
die folgende Form:
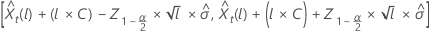
Dabei gilt:  steht für dar 100× 1– α/2)- d Perzentil aus der Standardnormalverteilung.
steht für dar 100× 1– α/2)- d Perzentil aus der Standardnormalverteilung.