Interpretieren der wichtigsten Ergebnisse für Prognose mit bestem ARIMA-Modell

Führen Sie die folgenden Schritte aus, um den Modellauswahlprozess und die Ergebnisse für die ARIMA-Analyse zu interpretieren. Zu den wichtigsten Ergebnissen gehören der Modell- ausgewählten Statistiken, der p-Wert, die Koeffizienten, die Ljung-Box-Chi-Quadrat-Statistiken und die Autokorrelationsfunktion der Residuen.

In diesem Thema

Schritt 1: Erwägen Sie, ein alternatives Modell zu verwenden
Schritt 2: Bestimmen, ob jeder Term im Modell signifikant ist
Schritt 3: Bestimmen, ob das Modell die Annahme der Analyse erfüllt

Schritt 1: Erwägen Sie, ein alternatives Modell zu verwenden

In der Tabelle Modellauswahl werden die Kriterien für jedes Modell in der Suche angezeigt. Die Tabelle zeigt die Reihenfolge der Terme, wobei p der autoregressive Term, d der differenzierende Term und q der gleitende Durchschnittsterm ist. Saisonale Begriffe verwenden Großbuchstaben und nicht saisonale Begriffe Kleinbuchstaben.

Anhand des AIC, des AICc und des BIC können Sie verschiedene Modelle vergleichen. Erwünscht sind kleinere Werte. Das Modell mit dem kleinsten Wert für eine Gruppe von Term ist jedoch nicht zwangsläufig gut an die Daten angepasst. Verwenden Sie Tests und Diagramme, um zu bewerten, wie gut das Modell zu den Daten passt. Standardmäßig gelten die ARIMA-Ergebnisse für das Modell mit dem besten AICc-Wert.

Wählen Sie diese Option Alternatives Modell auswählen , um ein Dialogfenster zu öffnen, das eine Tabelle Modellauswahl enthält. Vergleichen Sie die Kriterien, um Modelle mit ähnlicher Leistung zu untersuchen.

Verwenden Sie die ARIMA-Ausgabe, um zu überprüfen, ob die Begriffe im Modell statistisch signifikant sind und ob das Modell die Annahmen der Analyse erfüllt. Wenn keines der Modelle in der Tabelle gut zu den Daten passt, sollten Sie Modelle mit unterschiedlichen Ordnungen der Differenzierung in Betracht ziehen.

Betrachten Sie auch ein alternatives Modell, wenn ein alternatives Modell fast so gut abschneidet wie das beste Modell und niedrigere Ordnungen für die autoregressiven und gleitenden Durchschnittsterme aufweist. Ein Modell mit weniger Begriffen ist einfacher zu interpretieren und kann eine bessere Prognosefähigkeit haben. Modelle mit weniger Begriffen enthalten auch seltener redundante Begriffe. Beispielsweise sind saisonale autoregressive Begriffe manchmal redundant mit saisonalen gleitenden Durchschnittswerten. Redundante Begriffe machen manchmal die Schätzungen der Koeffizienten instabil. Instabile Koeffizienten können u. a. die folgenden Konsequenzen haben:

Die Koeffizienten sind anscheinend nicht signifikant, selbst wenn eine signifikante Beziehung zwischen dem Prädiktor und der Antwortvariablen besteht.
Die Koeffizienten für stark korrelierte Prädiktoren variieren erheblich von Stichprobe zu Stichprobe.
Das Entfernen von stark korrelierten Termen aus dem Modell hat schwerwiegende Auswirkungen auf die geschätzten Koeffizienten der anderen stark korrelierten Terme. Die Koeffizienten der stark korrelierten Terme können sogar ein falsches Vorzeichen aufweisen.

* WARNUNG * Nicht schätzbare ARIMA(p, d, q)-Modelle, die keinen konstanten Term enthalten:
(2; 1; 2)

Modellauswahl

Modell (d = 1)	Log-Likelihood	AICc	AIC	BIC
p = 0; q = 2*	-197,052	400,878	400,103	404,769
p = 1; q = 2	-196,989	403,311	401,978	408,199
p = 1; q = 0	-201,327	407,029	406,654	409,765
p = 2; q = 0	-200,239	407,251	406,477	411,143
p = 1; q = 1	-200,440	407,655	406,880	411,546
p = 2; q = 1	-201,776	412,884	411,551	417,773
p = 0; q = 1	-204,584	413,542	413,167	416,278
p = 0; q = 0	-213,614	429,350	429,229	430,784

Wichtigste Ergebnisse AICc, BIC, und AIC

Die ARIMA(0, 1, 2) hat den besten Wert von AICc. Die folgenden ARIMA-Ergebnisse beziehen sich auf das Modell ARIMA(0, 1, 2). Wenn das Modell nicht gut genug zu den Daten passt, sollten Sie andere Modelle mit ähnlicher Leistung in Betracht ziehen, z. B. das ARIMA(1, 1, 2)-Modell und das ARIMA-Modell (1, 1, 1). Wenn keines der Modelle gut genug zu den Daten passt, überlegen Sie, ob ein anderer Modelltyp verwendet werden soll.

Schritt 2: Bestimmen, ob jeder Term im Modell signifikant ist

Um zu bestimmen, ob die Assoziation zwischen der Antwortvariablen und jedem Term im Modell statistisch signifikant ist, vergleichen Sie den p-Wert für den Term mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese ist, dass sich der Term nicht signifikant von 0 unterscheidet, was darauf hinweist, dass keine Assoziation zwischen dem Term und der Antwort besteht. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 zeigt ein Risiko von 5% an, zu dem Schluss zu kommen, dass sich der Begriff nicht signifikant von 0 unterscheidet, wenn er signifikant von 0 abweicht.

p-Wert ≤ α:Die Term ist statistisch signifikant: Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass der Koeffizient statistisch signifikant ist.
p-Wert > α:Die Term ist statistisch nicht signifikant: Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass der Koeffizient statistisch signifikant ist. Es empfiehlt sich möglicherweise, das Modell ohne den Term erneut anzupassen.

Endgültige Schätzwerte der Parameter

Typ	Koef	SE Koef	t-Wert	p-Wert
AR 1	-0,504	0,114	-4,42	0,000
Konstante	150,415	0,325	463,34	0,000
Mittelwert	100,000	0,216

Wichtigste Ergebnisse: P, Koef

Der autoregressive Term weist einen p-Wert auf, der unterhalb des Signifikanzniveaus von 0,05 liegt. Sie können schlussfolgern, dass der Koeffizient für den autoregressiven Term statistisch signifikant ist und Sie den Term im Modell beibehalten sollten.

Schritt 3: Bestimmen, ob das Modell die Annahme der Analyse erfüllt

Verwenden Sie die Ljung-Box-Chi-Quadrat-Statistiken und die Autokorrelationsfunktion der Residuen, um zu ermitteln, ob das Modell die Annahme erfüllt, dass die Residuen unabhängig sind. Wenn sich die Annahme nicht bestätigt, ist das Modell möglicherweise nicht an die Daten angepasst und Sie sollten beim Interpretieren der Ergebnisse vorsichtig sein.

Ljung-Box-Chi-Quadrat-Statistiken: Um zu ermitteln, ob die Residuen unabhängig sind, vergleichen Sie den p-Wert jeder Chi-Quadrat-Statistik mit dem Signifikanzniveau. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie schlussfolgern, dass die Residuen unabhängig sind und das Modell die Annahme erfüllt.
Autokorrelationsfunktion der Residuen: Wenn keine signifikanten Korrelationen vorhanden sind, können Sie schlussfolgern, dass die Residuen unabhängig sind. Es kann jedoch sein, dass Sie ein oder zwei signifikante Korrelationen bei Lags höherer Ordnung feststellen, bei denen es sich nicht um saisonale Lags handelt. Diese Korrelationen sind in der Regel auf zufällige Fehler zurückzuführen und kein Anzeichen dafür, dass die Annahme nicht zutrifft. Sie können in diesem Fall schlussfolgern, dass die Residuen unabhängig sind.

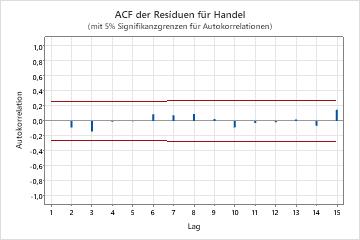
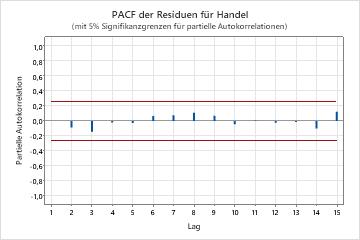
Wichtigste Ergebnisse: p-Wert, ACF der Residuen
In diesen Ergebnissen sind alle p-Werte für die Ljung-Box-Chi-Quadrat-Statistiken größer als 0,05, und keine der Korrelationen für die Autokorrelationsfunktion der Residuen ist signifikant. Sie können schlussfolgern, dass das Modell die Annahme von unabhängigen Residuen erfüllt.

Lag	12	24	36	48
Chi-Quadrat	4,05	12,13	25,62	32,09
DF	10	22	34	46
p-Wert	0,945	0,955	0,849	0,940