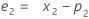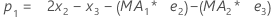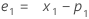In diesem Thema
Modellgleichung
Bei der zweifachen exponentiellen Glättung werden für jede Periode eine Niveaukomponente und eine Trendkomponente verwendet. Bei der zweifachen exponentiellen Glättung werden zwei Gewichtungen (auch Glättungsparameter genannt) verwendet, um die Komponenten für jede Periode zu aktualisieren. Die Gleichungen für die zweifache exponentielle Glättung lauten wie folgt:
Formel
Lt= αYt+ (1 – α) [Lt–1 + Tt–1]
Tt= γ [Lt – Lt–1] + (1 – γ) Tt–1
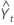 = Lt−1
+ Tt−1
= Lt−1
+ Tt−1
Wenn die erste Beobachtung mit 1 nummeriert wird, dann müssen die Niveau- und Trendschätzungen zum Zeitpunkt null initialisiert werden, um fortfahren zu können. Die verwendete Initialisierungsmethode bestimmt, mit welchem von zwei Verfahren die geglätteten Werte ermittelt werden: mit optimalen Gewichtungen oder mit angegebenen Gewichtungen.
Notation
| Begriff | Beschreibung |
|---|---|
| Lt | Niveau zum Zeitpunkt t |
| α | Gewichtung für das Niveau |
| Tt | Trend zum Zeitpunkt t |
| γ | Gewichtung für den Trend |
| Yt | Datenwert zum Zeitpunkt t |
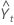 | Prognostizierte Wert zum Zeitpunkt t |
Gewichtungen
Optimale ARIMA-Gewichtungen
- Minitab passt ein ARIMA(0;2;2)-Modell an die Daten an, mit dem die Summe der quadrierten Fehler minimiert wird.
- Die Trend- und die Niveaukomponente werden anschließend per Rückwärtsprognose initialisiert.
Angegebene Gewichtungen
- Minitab passt ein lineares Regressionsmodell an die Zeitreihendaten (y-Variable) im Vergleich mit der Zeit (x-Variable) an.
- Die Konstante (Schnittpunkt mit der y-Achse) aus dieser Regression ist die Anfangsschätzung der Niveaukomponente, der Steigungskoeffizient die Anfangsschätzung der Trendkomponente.
Wenn Sie Gewichtungen angeben, die einem ARIMA(0;2;2)-Modell mit gleichen Wurzeln entsprechen, entspricht die Holt-Methode der spezifischeren Brown-Methode.1.
Methode zur Berechnung von Anfangswerten für Niveau und Trend
können Schätzwerte für Niveau und Trend speichern. Minitab verwendet eine der folgenden Methoden, um die Werte in der ersten Zeile dieser Spalten zu berechnen, abhängig von den Optionen, die Sie im Dialogfeld festlegen.
Wenn Sie die Option Optimale ARIMA in Zweifache exponentielle Glättung auswählen, verwendet Minitab die folgende Methode, um die ersten Werte von Niveau und Trend zu berechnen. Sie können diese Schritte von Hand ausführen.
- Wählen Sie aus, um die optimalen Gewichtungswerte mit ARIMA zu berechnen. Vervollständigen Sie das Dialogfeld wie folgt:
- Geben Sie im Feld Autoregressiv den Wert 0 ein.
- Geben Sie im Feld Differenz den Wert 2 ein.
- Geben Sie im Feld Gleitender Durchschnitt den Wert 2 ein.
- Deaktivieren Sie Konstanten Term in Modell einbinden.
- Klicken Sie auf Speichern und aktivieren Sie Residuen. Klicken Sie in den einzelnen Dialogfeldern auf OK.
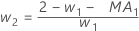
- Minitab verwendet die MA-Werte aus der ARIMA-Ausgabe,
um die optimalen Gewichtungen wie folgt zu berechnen:
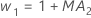
- Anschließend rechnet Minitab anhand von Daten aus späteren Beobachtungen bis zur ersten Beobachtung zurück:
Dabei gilt Folgendes:
Begriff Beschreibung pi ist der prognostizierte Wert der i-ten geglätteten Beobachtung xi ist der i-ten Beobachtungen in der Zeitreihe. ei ist der Wert des i-ten Residuums, gespeichert aus obiger ARIMA -
- Minitab berechnet den Anfangswert für Niveau (L1):

- Minitab berechnet den Anfangswert für Trend (T1):
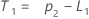
- Erstellen Sie eine Spalte mit Zeitindizes, die der Länge der Spalte mit Zeitreihendaten entspricht. Eine Spalte mit ganzen Zahlen von 1 bis n ist ausreichend.
- Wählen Sie aus.
- Geben Sie in Antworten die Spalte mit Zeitreihendaten ein. Geben Sie in Stetige Prädiktoren die Spalte der Zeitindizes ein.
- Klicken Sie auf Speichern und aktivieren Sie Koeffizienten. Klicken Sie in den einzelnen Dialogfeldern auf OK.
- Der Anfangswert für das Niveau ist:
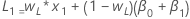
- Der Anfangswert für Trend ist:
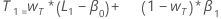 Dabei gilt Folgendes:
Dabei gilt Folgendes:Begriff Beschreibung L1 ist der Anfangswert für das Niveau x1 ist der Wert der ersten Beobachtung in der Zeitreihe T1 ist der Anfangswert für Trend wL ist der Gewichtungswert für das Niveau wT ist der Gewichtungswert für den Trend β0 ist der Koeffizient des konstanten Terms im Regressionsmodell β1 ist der Koeffizient für den Prädiktorterm im Regressionsmodell
Prognosen
Bei der zweifachen exponentiellen Glättung werden Prognosen anhand der Niveau- und Trendkomponente erstellt. Die Prognose für m Perioden ab einem bestimmten Zeitpunkt t lautet wie folgt:
Formel
Lt + mTt
Für die Glättung werden die Daten bis zum Prognoseursprung verwendet.
Notation
| Begriff | Beschreibung |
|---|---|
| Lt | Niveau zum Zeitpunkt t |
| Tt | Trend zum Zeitpunkt t |
Prognosegrenzen
Formel
- Obergrenze = Prognose + 1,96 × dt × MAD
- Untergrenze = Prognose – 1,96 × dt × MAD
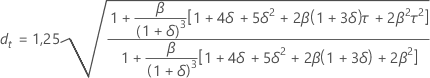
Notation
| Begriff | Beschreibung |
|---|---|
| β | max{α, γ) |
| δ | 1 – β |
| α | Glättungskonstante für Niveau |
| γ | Glättungskonstante für Trend |
| τ |  |
| b0(T) | 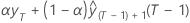 |
| b1(T) | 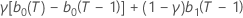 |
MAPE
Der mittlere absolute prozentuale Fehler (MAPE) ist eine Maßzahl für die Genauigkeit der angepassten Zeitreihenwerte. MAPE drückt die Genauigkeit als Prozentsatz aus.
Formel
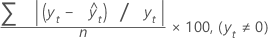
Notation
| Begriff | Beschreibung |
|---|---|
| yt | tatsächlicher Wert zum Zeitpunkt t |
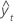 | angepasster Wert |
| n | Anzahl der Beobachtungen |
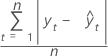
MAD
Die mittlere absolute Abweichung (MAD) ist eine Maßzahl für die Genauigkeit der angepassten Zeitreihenwerte. MAD drückt die Genauigkeit in der gleichen Einheit wie die Daten aus, wodurch der Fehlerbetrag leichter erfasst werden kann.
Formel
Notation
| Begriff | Beschreibung |
|---|---|
| yt | tatsächlicher Wert zum Zeitpunkt t |
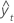 | angepasster Wert |
| n | Anzahl der Beobachtungen |
MSD
Die mittlere quadrierte Abweichung (MSD) wird immer mit demselben Nenner n berechnet, unabhängig vom Modell. MSD ist bei ungewöhnlich großen Prognosefehlern ein empfindlicheres Maß als MAD.
Formel
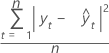
Notation
| Begriff | Beschreibung |
|---|---|
| yt | tatsächlicher Wert zum Zeitpunkt t |
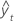 | angepasster Wert |
| n | Anzahl der Beobachtungen |