Ein Umweltingenieur misst an zwei Orten eines Flusses über einen Zeitraum von 15 Tagen die im Wasser enthaltenen Schwebstoffe. Er erwartet eine Korrelation zwischen den beiden Orten. Da sich ein Ort weiter flussabwärts befindet, vermutet der Techniker, dass das Korrelationsmuster zu der Zeit passt, die das Wasser zum Zurücklegen der Strecke zwischen den beiden Orten benötigt.
Der Techniker führt eine Kreuzkorrelationsanalyse durch, um zu ermitteln, wie viele Tage Wasser benötigt, um von einem flussaufwärts gelegenen Ort zu einem flussabwärts gelegenen Ort zu gelangen.
- Öffnen Sie die Beispieldaten Flussschwebstoffe.MTW.
- Wählen Sie aus.
- Geben Sie im Feld Erste Datenreihe die Spalte Flussaufwärts ein.
- Geben Sie im Feld Zweite Datenreihe die Spalte Flussabwärts ein.
- Klicken Sie auf OK.
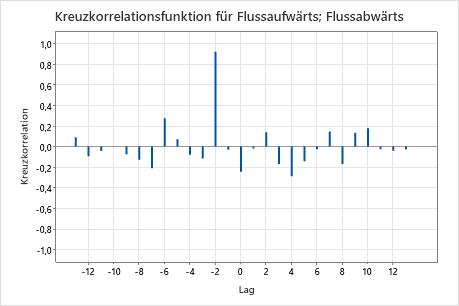
Interpretieren der Ergebnisse
Die Kreuzkorrelationsfunktion weist eine große Spitze bei einem Lag von -2 auf. Der Wert von ca. 0,92 weicht signifikant von 0 ab, da er größer ist als 0,55 = 
. Hierbei handelt es sich um eine Faustformel, die angibt, dass die Korrelation mehr als 2 Standardabweichungen von 0 beträgt. Der Techniker kann schlussfolgern, dass das Wasser 2 Tage benötigt, um vom flussaufwärts gelegenen Ort zum flussabwärts gelegenen Ort zu gelangen.
Kreuzkorrelationen
| Lag | KKF |
|---|---|
| -13 | 0,088605 |
| -12 | -0,094967 |
| -11 | -0,044034 |
| -10 | 0,002249 |
| -9 | -0,075707 |
| -8 | -0,129418 |
| -7 | -0,211479 |
| -6 | 0,274646 |
| -5 | 0,070625 |
| -4 | -0,080266 |
| -3 | -0,116391 |
| -2 | 0,919857 |
| -1 | -0,030654 |
| 0 | -0,244537 |
| 1 | -0,020511 |
| 2 | 0,137672 |
| 3 | -0,169664 |
| 4 | -0,288815 |
| 5 | -0,143804 |
| 6 | -0,027369 |
| 7 | 0,144552 |
| 8 | -0,169233 |
| 9 | 0,133472 |
| 10 | 0,176201 |
| 11 | -0,026856 |
| 12 | -0,041351 |
| 13 | -0,026638 |
