In diesem Thema
Box-Cox-Transformation
Die Box-Cox-Transformation wird durch die folgende Formel ausgedrückt:

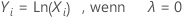
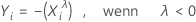
Hierbei ist Xi ein ursprünglicher Datenwert und λ der Parameter für die Transformation. Wenn die Analyse nach dem optimalen Wert von λsucht, rundet die Analyse den optimalen Wert von λ auf 0,5 oder auf die nächste ganze Zahl, um die Transformation durchzuführen.
Gängige λ-Werte
| λ | Transformation |
|---|---|
| 2 | 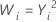 |
| 0.5 |  |
| 0 |  |
| -1 |  |
Suche nach dem optimalen λ
- Definieren Sie das Kriterium für den optimalen Wert als minimalen Variationskoeffizienten.
- Teilen Sie die Reihe in H-Unterreihen auf.
- Verwenden Sie die Methode von Brent, um den Wert von λ zu finden, der den Variationskoeffizienten minimiert.
In den folgenden Abschnitten werden die Teilreihen und der Variationskoeffizient definiert.
Unterreihen
Unterteilen Sie die Reihe in Unterreihen nach Saisonzeitraum. Wenn sich der Jahreszeitraum nicht gleichmäßig in die Reihe aufteilt, lassen Sie die verbleibenden Beobachtungen vom Anfang der Reihe weg. Wenn die Spezifikationen für die Analyse keinen saisonalen Zeitraum enthalten, setzen Sie den Jahreszeitraum = 2.
Nehmen wir beispielsweise eine ursprüngliche Zeitreihe mit 10 Beobachtungen und einem saisonalen Zeitraum von 4 an: {5, 6, 3, 2, 9, 8, 1, 7, 10, 4}. Die Anzahl der Unterreihen beträgt 10 modulo 4 = 2. Da 4 nicht gleichmäßig in 10 unterteilt ist, verwenden Sie nur die letzten 8 Beobachtungen, um die Unterreihe zu bilden. Die Unterreihen sind {3, 2, 9, 8} und {1, 7, 10, 4}.
Fehlende Werte
Wenn eine Unterreihe 1 oder mehr fehlende Werte enthält, lassen Sie die Unterreihe bei der Suche nach dem optimalen Wert von λ aus den Berechnungen aus. Die Suche erfordert mindestens 2 Unterreihen ohne fehlende Werte.
Variationskoeffizient
Verwenden Sie die folgenden Definitionen, um den Variationskoeffizienten zu berechnen:| Begriff | Beschreibung |
|---|---|
| X1, X2, … XN | die Beobachtungen in der ursprünglichen Zeitreihe |
| P | Der Jahreszeitraum der ursprünglichen Zeitreihe |
| Xh, i | Die i-ten Beobachtung in der Unterreihe h, wobei i=1, ..., P und h=1, ..., H |
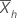 | das Stichprobenmittel der h-ten Unterreihe |
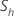 | die Stichprobenstandardabweichung der h-ten Unterreihe |
Die folgenden Gleichungen definieren die Statistiken für jede Teilreihe:
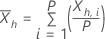
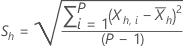
Für ein gegebenes λ und für h=1, ..., H verwendet folgende Definition:
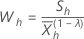
Berechnen Sie den Stichprobendurchschnitt und die Stichprobenstandardabweichung für die W-Statistik :

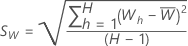

Verwenden Sie die Methode von Brent, um den Wert von λ zu finden, der den CV im Intervall von den Spezifikationen für die Analyse minimiert. Die Analyse rundet den optimalen Wert von λ auf 0,5 oder auf die nächste ganze Zahl, um die Transformation durchzuführen.
