Außerdem wurden für jeden Monat Daten zur Anzahl der Verkaufsstellen erhoben. Der Analyst möchte ein ARIMA-Modell verwenden, um Prognosen für die Daten zu generieren. In einem Zeitreihendiagramm sieht der Analyst, dass der Unterschied zwischen den hohen und niedrigen saisonalen Spitzen im Laufe der Zeit zunimmt. Dieses Muster zeigt an, dass die Varianz nicht stationär ist. Der Analyst führt eine Box-Cox-Transformation durch, um die Varianz stationär zu machen, bevor der Analyst dem ARIMA-Modell entspricht.
- Öffnen Sie die Beispieldaten Fluggaste.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Datenreihe den Wert Anzahl der Passagiere ein.
- Geben Sie im Feld Saisonale Periode den Wert 12 ein.
- Wählen Sie diese Option aus Optimales λ , damit Minitab Statistical Software nach einer zu verwendenden Transformation sucht.
- Geben Sie im Feld Zeitstempelspalte für Zeitskala den Wert Datum ein.
- Geben Sie im Feld Transformierte Datenreihe speichern in den Wert Umgewandelt ein. Klicken Sie auf OK.
Interpretieren der Ergebnisse
Die Tabelle Methode zeigt die Einstellungen für die Analyse und den Wert von λ für die Transformation.
In diesen Ergebnissen ist der saisonale Zeitraum 12 und die Analyse sucht nach einem λ-Wert zwischen dem Standardbereich von -1 und 2. Der optimale λ-Wert ist ungefähr -0,14. Die Analyse rundet den Wert auf 0 und verwendet die natürliche Log-Transformation.
Methode
| Saisonale Periode | 12 |
|---|---|
| Optimales λ aus Intervall auswählen | [-1; 2] |
| Optimales λ | -0,144439 |
| Gerundetes optimales λ | 0 |
| Transformierte Datenreihe = ln(Anzahl der Passagiere) |
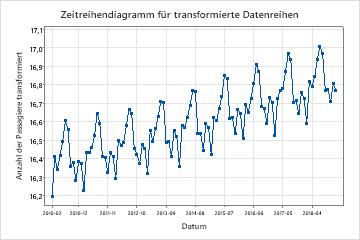
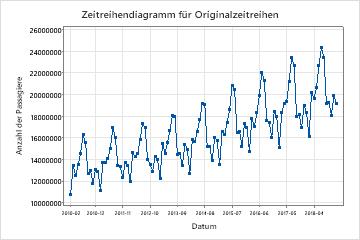
Vergleichen Sie die Zeitreihe der Originalreihe mit dem Zeitreihendiagramm der transformierten Reihe, um sicherzustellen, dass die Transformation die Varianz stationär macht.
In diesen Ergebnissen zeigt das Zeitreihendiagramm der Originalserie die nichtstationäre Varianz. In diesen Daten nimmt die Differenz zwischen den Hoch- und Tiefpunkten in einem saisonalen Zyklus im Laufe der Zeit zu. Dieses Muster zeigt, dass die Varianz im Laufe der Zeit zunimmt.
Untersuchen Sie das Zeitreihendiagramm der transformierten Reihe, um sicherzustellen, dass die Transformation die Varianz stationär macht.
In diesen Ergebnissen zeigt das Zeitreihendiagramm der transformierten Reihe eine annähernd gleichmäßige Differenz zwischen den Hoch- und Tiefpunkten in den saisonalen Zyklen. Dieses Muster zeigt, dass die Transformation die Varianz stationär macht.
Untersuchen Sie auch das Zeitreihendiagramm der transformierten Daten, um andere wichtige Merkmale der transformierten Reihe zu bewerten. Zu den Annahmen für ein ARIMA-Modell gehört beispielsweise, dass die Reihe neben einer stationären Varianz auch einen stationären Mittelwert aufweist. Wenn ein Zeitreihendiagramm der transformierten Reihe zeigt, dass die transformierte Reihe keinen stationären Mittelwert hat, versuchen Sie Erweiterter Dickey-Fuller-Test zu sehen, ob die Differenzierung der Daten den Mittelwert der Reihe stationär macht.
In diesen Ergebnissen zeigt die transformierte Reihe einen Aufwärtstrend. Dieses Muster zeigt, dass der Mittelwert der Serie nicht stationär ist. Verwenden Sie die Spalte auf der gespeicherten Spalte der transformierten Daten, um zu bestimmen, ob Differenzierung die Erweiterter Dickey-Fuller-Test Reihe stationär macht.