Bei der Autokorrelationsfunktion handelt es sich um ein Maß für die Korrelation zwischen den um k Zeiteinheiten auseinander liegenden Beobachtungen einer Zeitreihe (yt und yt–k).
Interpretation
Verwenden Sie die Autokorrelationsfunktion zusammen mit der partiellen Autokorrelationsfunktion, um ARIMA-Modelle zu bestimmen. Untersuchen Sie die Spitzen bei jedem Lag, um zu ermitteln, ob sie signifikant sind. Eine signifikante Spitze reicht über die Signifikanzgrenzen hinaus, was darauf hindeutet, dass die Korrelation für diesen Lag ungleich null ist.
Hinweis
Bevor Sie das Autokorrelationsdiagramm interpretieren, sollten die Daten stationär sein. Eine stationäre Zeitreihe weist einen Mittelwert, eine Varianz und eine Autokorrelationsfunktion auf, die im Verlauf der Zeit im Wesentlichen konstant bleiben. Weitere Informationen finden Sie unter Überlegungen zu Daten für Autokorrelationsfunktion.
| Muster | Bedeutung des Musters | Beispiel |
|---|---|---|
| Große Spitze bei Lag 1, die nach einigen Lags abnimmt. | Ein autoregressiver Term in den Daten. Ermitteln Sie mit Hilfe der partiellen Autokorrelationsfunktion die Ordnung des autoregressiven Terms. | 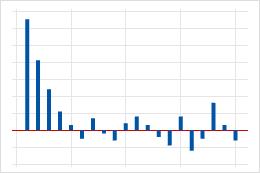 |
| Große Spitze bei Lag 1, gefolgt von einer abnehmenden Welle, die zwischen positiven und negativen Korrelationen wechselt. | Ein autoregressiver Term höherer Ordnung in den Daten. Ermitteln Sie mit Hilfe der partiellen Autokorrelationsfunktion die Ordnung des autoregressiven Terms. | 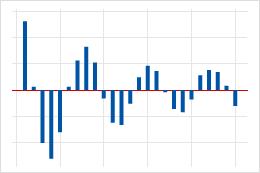 |
| Signifikante Korrelationen bei Lag 1 oder 2, gefolgt von nicht signifikanten Korrelationen. | Ein Term des gleitenden Durchschnitts in den Daten. Die Anzahl der signifikanten Korrelationen gibt die Ordnung des Terms des gleitenden Durchschnitts an. | 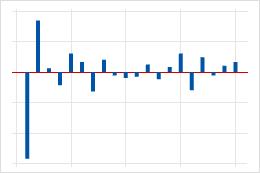 |
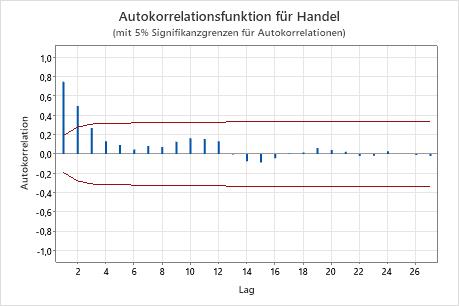
Dieses Diagramm weist eine signifikante Korrelation bei lag eins auf, die nach einigen Lecks abnimmt. Dieses Muster deutet auf einen Auto degressiven Term hin. Sie sollten mithilfe der partiellen Autokorrelationsfunktion die Ordnung des autoregressiven Terms ermitteln.
