Regressionsmodelle
| Begriff | Beschreibung |
|---|---|
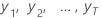 | die beobachteten Zeitreihenwertezum Zeitpunkt = 1, ..., T |
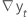 | die Differenz zweier aufeinanderfolgender Beobachtungen zum Zeitpunkt t, 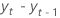 , wobei t = 2, ..., T , wobei t = 2, ..., T |
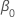 | die konstanten Term im Regressionsmodell |
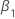 | ist der Koeffizient eines linearen Zeittrends im Regressionsmodell |
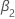 | ist der Koeffizient eines quadratisch Zeittrends im Regressionsmodell |
 | die Verzögerungsreihenfolge des autoregressiven Prozesses |
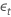 | der seriell unabhängige Fehlerterm zum Zeitpunkt t für t = 2, ..., T |
- Ein Modell mit nur einem konstanten Koeffizienten

- Ein Modell mit einem konstanten Koeffizienten und einem linearen Koeffizienten
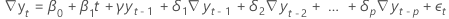
- Ein Modell mit einem konstanten Koeffizienten, linearen Koeffizienten und einem quadratischen Koeffizienten

- Ein Modell ohne Regressionskoeffizienten
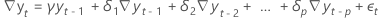
Hypothesen
Jeder Augmented Dickey-Fuller-Test verwendet die folgenden Hypothesen:
Nullhypothese, H0: 
Alternativhypothese, H1: 
Die Nullhypothese besagt, dass sich eine Einheitenwurzel in der Zeitreihenstichprobe befindet, was bedeutet, dass der Mittelwert der Daten nicht stationär ist. Das Ablehnen der Nullhypothese zeigt an, dass der Mittelwert der Daten stationär oder trendstationär ist, abhängig vom Modell für den Test.
Teststatistik

Dabei gilt Folgendes:
| Begriff | Beschreibung |
|---|---|
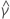 | die Schätzung des kleinsten quadratischen Koeffizienten der 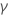 Koeffizienten Koeffizienten |
 | Der Standardfehler der Schätzung der kleinsten Quadrate der 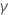 Koeffizient aus dem Regressionsmodell Koeffizient aus dem Regressionsmodell |
MacKinnon's annähernde p-Werte
Nach der Nullhypothese folgt die asymptotische Verteilung der Teststatistik keiner Standardverteilung. Fuller (1976)1 stellt eine Tabelle mit gemeinsamen Perzentilen der asymptotischen Verteilung bereit. MacKinnon (19942, 20103) wendet Antwortflächennäherungen auf simulierte Daten an, um einen ungefähren p-Wert für einen beliebigen Wert der ADF-Teststatistik bereitzustellen.
Wenn die Spezifikationen für die Analyse 0,01, 0,05 oder 0,1 als Signifikanzniveau verwenden, vergleicht die Auswertung der Nullhypothese die Teststatistik mit dem kritischen Wert für dieses Signifikanzniveau. Wenn die Teststatistik kleiner oder gleich dem kritischen Wert ist, verwerfen Sie die Nullhypothese.
Wenn die Spezifikationen für die Analyse ein anderes Signifikanzniveau ergeben, dann vergleicht die Auswertung der Nullhypothese den ungefähren p-Wert mit dem Signifikanzniveau. Wenn der p-Wert kleiner als der Signifikanzniveau ist, weisen Sie die Nullhypothese zurück.
Kritische Werte für die Signifikanzstufen 0,01, 0,05 und 0,1
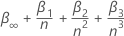
wobei n die Anzahl der Beobachtungen ist, die die Analyse verwendet, um das Regressionsmodell anzupassen. Die Werte für 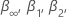 und
und 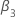 stammen von Tabellen in MacKinnon (2010). Wenn die Teststatistik kleiner oder gleich dem kritischen Wert ist, verwerfen Sie die Nullhypothese.
stammen von Tabellen in MacKinnon (2010). Wenn die Teststatistik kleiner oder gleich dem kritischen Wert ist, verwerfen Sie die Nullhypothese.
ungefähre p-Wert
Die Berechnung des ungefähren p-Wertes stammt aus Mackinnon (1994). Vergleichen Sie den p-Wert mit dem Signifikanzniveau, um eine Entscheidung zu treffen. Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück.
Bestimmung der Verzögerungsreihenfolge

Die Auswahl der Verzögerungsreihenfolge hängt vom Kriterium in den Spezifikationen der Analyse ab. Wenn die Spezifikationen für die Analyse kein Kriterium enthalten, ist das Regressionsmodell für den Test die maximale Ordnung von p.
In den Berechnungen zur Bestimmung der Verzögerungsreihenfolge hängt die Anzahl der Beobachtungen von der maximalen Verzögerungsreihenfolge ab, so dass m = n – p – 1.
| Begriff | Beschreibung |
|---|---|
| n | Gesamtzahl der Beobachtungen |
| p | die maximale Lag-Ordnung der differenzierten Terme, die sich im Modell befinden |
Die Berechnung jedes Kriteriums folgt:
Akaike Information Criterion (AIC)
Die Analyse wertet ein Regressionsmodell für jede Lag-Ordnung in den Spezifikationen der Analyse aus. Die Lag-Ordnung für den Test ist das Regressionsmodell mit dem Minimalwert des AIC.
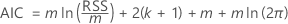
Dabei gilt Folgendes:
| Begriff | Beschreibung |
|---|---|
| m | Die Anzahl der Beobachtungen, die von der maximalen Lag-Ordnung abhängt |
| k | Die Anzahl der Koeffizienten im Modell, einschließlich der Konstante, wenn das Regressionsmodell eine Konstante ungleich Null aufweist |
| RSS | die Restsumme der Quadrate des Regressionsmodells |
Bayessche Informationskriterium (BIC)
Die Analyse wertet ein Regressionsmodell für jede Lag-Ordnung in den Spezifikationen der Analyse aus. Die Lag-Ordnung für den Test ist das Regressionsmodell mit dem Minimalwert des BIC.
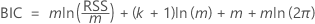
Dabei gilt Folgendes:
| Begriff | Beschreibung |
|---|---|
| m | Die Anzahl der Beobachtungen, die von der maximalen Lag-Ordnung abhängt |
| k | Die Anzahl der Koeffizienten im Modell, einschließlich der Konstante, wenn das Regressionsmodell eine Konstante ungleich Null aufweist |
| RSS | die Restsumme der Quadrate des Regressionsmodells |
t-Statistik
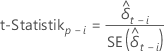
wobei i = 1,…, p
| Begriff | Beschreibung |
|---|---|
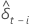 | die Schätzung der kleinsten Quadrate der  Koeffizient im Regressionsmodell Koeffizient im Regressionsmodell |
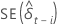 | Der Standardfehler der Schätzung der kleinsten Quadrate der  Koeffizient im Regressionsmodell Koeffizient im Regressionsmodell |
