Schritt 1: Bestimmen Sie, ob die Daten stationär oder trendstationär sind
Die Augmented Dickey-Fuller-Testtabelle enthält die Hypothesen, eine Teststatistik, einen p-Wert und eine Empfehlung, ob nicht-saisonale Unterschiede berücksichtigt werden sollten, um die Daten stationär zu machen.
Die Teststatistik bietet eine Möglichkeit, die Nullhypothese auszuwerten. Teststatistiken, die kleiner oder gleich dem kritischen Wert sind, liefern Beweise für die Nullhypothese.
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Um festzustellen, ob die Daten differenziert werden sollen, vergleichen Sie die Teststatistik mit dem kritischen Wert oder den p-Wert mit Ihrem Signifikanzniveau. Da der p-Wert mehr Näherungswerte enthält, verwendet die Empfehlung aus der Analyse den kritischen Wert, um die Nullhypothese zu bewerten, wenn das Signifikanzniveau 0,01, 0,05 oder 0,10 beträgt. Normalerweise ist die Schlussfolgerung für den kritischen Wert und den p-Wert gleich. Die Nullhypothese ist, dass die Daten nicht stationär sind, was impliziert, dass die Differenzierung ein vernünftiger Schritt ist, um zu versuchen, die Daten stationär zu machen.
- p-Wert ≤ Signifikanzniveau
- Teststatistik ≤ kritischen Wert
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist oder wenn die Teststatistik kleiner oder gleich dem kritischen Wert ist, weisen Sie die Nullhypothese zurück. Da die Daten den Nachweis erbringen, dass die Daten stationär sind, lautet die Empfehlung der Analyse, ohne Unterschied fortzufahren.
- p-Wert > Signifikanzniveau
- Teststatistik > kritischen Wert
- Wenn der p-Wert größer als das Signifikanzniveau ist oder wenn die Teststatistik größer als dem kritischen Wert ist, weisen Sie die Nullhypothese nicht zurück. Da die Daten keinen Beweis dafür liefern, dass die Daten stationär sind, besteht die Empfehlung der Analyse darin, festzustellen, ob die Differenzierung den Mittelwert der Daten stationär macht.
Wenn die Daten stationär sind, empfiehlt der Test keine Differenzierung. Erkunden Sie ARIMA-Modelle, die keine differenzierenden Begriffe enthalten. Wenn die Daten nicht stationär sind, untersuchen Sie ARIMA-Modelle, die unterschiedliche Begriffe enthalten. Verwenden Sie das Zeitreihendiagramm der differenzierten Daten, um zu sehen, ob die Unterschiede zwischen aufeinanderfolgenden Beobachtungen ein stationärer Datensatz sind. Wenn die differenzierten Daten stationär sind, sind ARIMA-Modelle mit einem Differenzierungsterm erster Ordnung sinnvoll zu berücksichtigen.
In diesen Ergebnissen ist der Teststatistik 2,29045 und somit größer als dem kritischen Wert von ungefähr -2,96053. Da die Ergebnisse die Nullhypothese, dass die Daten nicht stationär sind, nicht ablehnen, besteht die Empfehlung des Tests darin, eine Differenzierung in Betracht zu ziehen, um die Daten stationär zu machen.
Erweiterter Dickey-Fuller-Test
| Nullhypothese: | Daten sind nicht stationär |
|---|---|
| Alternativhypothese: | Daten sind stationär |
| Teststatistik | p-Wert | Empfehlung |
|---|---|---|
| 2,29045 | 0,999 | Teststatistik > kritischer Wert von -2,96053. |
| Signifikanzniveau = 0,05 | ||
| Nullhypothese nicht zurückweisen. | ||
| Erwägen Sie eine Differenzbildung, um die Daten stationär zu machen. |
Schritt 2: Untersuchen der Auswirkungen der Differenzierung der Daten
Wenn die Schlussfolgerung des Tests eine Differenzierung unterstützt, untersuchen Sie die Diagramme der differenzierten Daten auf Merkmale von Daten, die nicht stationär sind. Ein Trend im Zeitreihendiagramm ist ein Beispiel für ein Muster, das angibt, dass der Mittelwert der Daten nicht stationär ist. Auf dem ACF-Diagramm weisen große Spitzen, die langsam abnehmen, auch auf Daten hin, die nicht stationär sind. Wenn Sie diese Muster in den differenzierten Daten sehen, überlegen Sie, ob Sie ein ARIMA-Modell mit einer zweiten Ordnung der Differenzierung ausstatten möchten. In der Regel reichen 1 oder 2 Differenzierungsordnungen aus, um eine angemessene Anpassung an die Daten zu gewährleisten.
Wenn die differenzierten Daten stationär sind, besteht ein vernünftiger Ansatz darin, eine einzige Ordnung der nicht-saisonalen Differenzierung in ein ARIMA-Modell aufzunehmen. Weitere Informationen zu ARIMA-Modell finden Sie unter Übersicht über ARIMA.
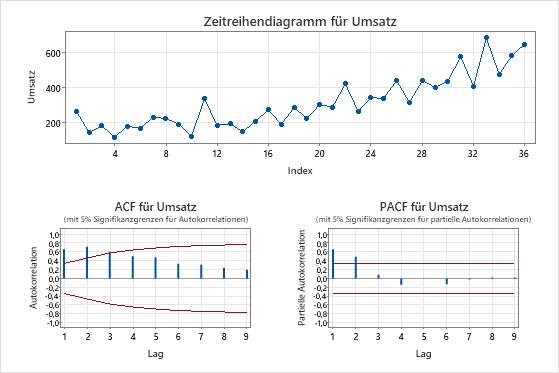
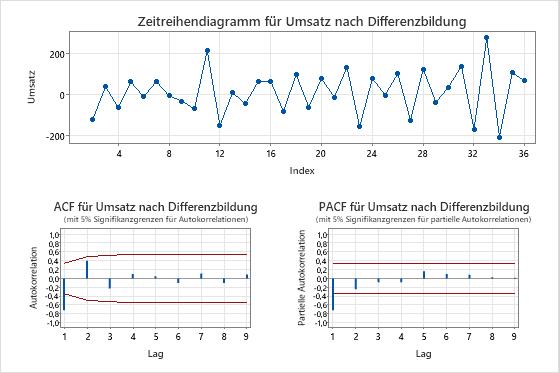
Die Zeitreihendiagramme zeigen das Ergebnis der Differenzierung. In diesen Ergebnissen zeigt das Zeitreihendiagramm der Originaldaten einen klaren Trend. Das Zeitreihendiagramm der differenzierten Daten zeigt die Unterschiede zwischen aufeinanderfolgenden Werten. Die differenzierten Daten erscheinen stationär, da die Punkte einem horizontalen Pfad ohne offensichtliche Muster in der Variation folgen.
Die ACF-Diagramme zeigen auch den Effekt der Differenzierung. In diesen Ergebnissen zeigt das ACF-Diagramm der Originaldaten langsam verringerte Spitzen über Lags hinweg. Dieses Muster zeigt an, dass die Daten nicht stationär sind. Im ACF-Diagramm der differenzierten Daten befindet sich die einzige Spitze, die sich signifikant von 0 unterscheidet, bei Verzögerung 1.
In diesen Ergebnissen bestätigen die Zeitreihendiagramme und die ACF-Diagramme die Testergebnisse. Daher ist es ein vernünftiger Ansatz, die Daten zu differenzieren und dann ein autoregressives und gleitendes Durchschnittsmodell anzupassen, um Prognosen zu erstellen.