In diesem Thema
Tabelle der Methode
In der Tabelle Methode werden die Einstellungen für die Analyse und die ausgewählte Verzögerungsreihenfolge angezeigt.
In diesen Ergebnissen ist die maximale Verzögerungsreihenfolge, die die Analyse auswertet, 9. Die Analyse verwendet das Modell mit der höchsten Verzögerungsreihenfolge von 4, um die Testergebnisse zu berechnen.
Methode
| Maximale Lag-Ordnung für Terme im Regressionsmodell | 9 |
|---|---|
| Kriterium für Auswahl der Lag-Ordnung | Minimales AIC |
| Zusätzliche Terme | Konstante |
| Ausgewählte Lag-Ordnung | 4 |
| Verwendete Zeilen | 36 |
Erweiterter Dickey-Fuller-Testtisch
Die Augmented Dickey-Fuller-Testtabelle enthält die Hypothesen, eine Teststatistik, einen p-Wert und eine Empfehlung, ob eine Differenzierung in Betracht gezogen werden sollte, um die Reihe stationär zu machen.
Die Teststatistik bietet eine Möglichkeit, die Nullhypothese auszuwerten. Teststatistiken, die kleiner oder gleich dem kritischen Wert sind, liefern Beweise für die Nullhypothese.
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Um festzustellen, ob die Daten differenziert werden sollen, vergleichen Sie die Teststatistik mit dem kritischen Wert oder den p-Wert mit Ihrem Signifikanzniveau. Da der p-Wert mehr Näherungswerte enthält, verwendet die Empfehlung aus der Analyse den kritischen Wert, um die Nullhypothese zu bewerten, wenn das Signifikanzniveau 0,01, 0,05 oder 0,10 beträgt. Normalerweise ist die Schlussfolgerung für den kritischen Wert und den p-Wert gleich. Die Nullhypothese ist, dass die Daten nicht stationär sind, was impliziert, dass die Differenzierung ein vernünftiger Schritt ist, um zu versuchen, die Daten stationär zu machen.
- p-Wert ≤ Signifikanzniveau
- Teststatistik ≤ kritischen Wert
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist oder wenn die Teststatistik kleiner oder gleich dem kritischen Wert ist, weisen Sie die Nullhypothese zurück. Da die Daten den Nachweis erbringen, dass die Daten stationär sind, lautet die Empfehlung der Analyse, ohne Unterschied fortzufahren.
- p-Wert > Signifikanzniveau
- Teststatistik > kritischen Wert
- Wenn der p-Wert größer als das Signifikanzniveau ist oder wenn die Teststatistik größer als dem kritischen Wert ist, weisen Sie die Nullhypothese nicht zurück. Da die Daten keinen Beweis dafür liefern, dass die Daten stationär sind, besteht die Empfehlung der Analyse darin, festzustellen, ob die Differenzierung den Mittelwert der Daten stationär macht.
In diesen Ergebnissen ist der Teststatistik 2,29045 und somit größer als dem kritischen Wert von ungefähr -2,96053. Da die Ergebnisse die Nullhypothese, dass die Daten nicht stationär sind, nicht ablehnen, besteht die Empfehlung des Tests darin, eine Differenzierung in Betracht zu ziehen, um die Daten stationär zu machen.
Erweiterter Dickey-Fuller-Test
| Nullhypothese: | Daten sind nicht stationär |
|---|---|
| Alternativhypothese: | Daten sind stationär |
| Teststatistik | p-Wert | Empfehlung |
|---|---|---|
| 2,29045 | 0,999 | Teststatistik > kritischer Wert von -2,96053. |
| Signifikanzniveau = 0,05 | ||
| Nullhypothese nicht zurückweisen. | ||
| Erwägen Sie eine Differenzbildung, um die Daten stationär zu machen. |
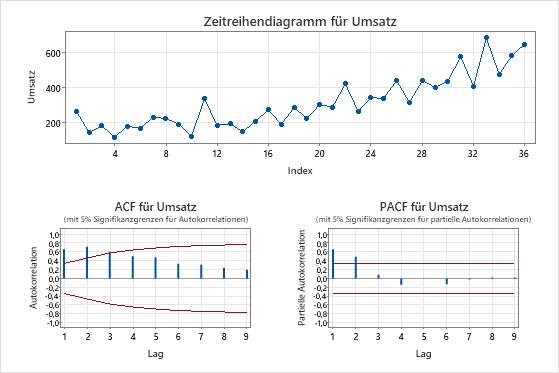
Plots der Originalserie
- Zeitreihendiagramm
- Verwenden Sie das Zeitreihendiagramm der Originalreihe, um die Eigenschaften der Originaldaten zu untersuchen. Ein Trend ist ein Beispiel für ein Muster, das auf einen nicht stationären Mittelwert hinweist. Verwenden Sie die Differenzierung, um zu versuchen, den Mittelwert stationär zu machen.
- ACF-Diagramm
- Verwenden Sie die Autokorrelationsfunktion (ACF) aus den Originaldaten, um nach einem Muster zu suchen, das angibt, dass der Mittelwert der Daten nicht stationär ist. Ein häufiges Muster sind große Spitzen über Lags, die sehr langsam aussterben.
- PACF-Diagramm
- Normalerweise verwenden Sie die partielle Autokorrelationsfunktion (PACF) stationärer Daten, um nach Mustern zu suchen, die auf das Vorhandensein autoregressiver Terme in einem ARIMA-Modell hinweisen. Wenn die Originaldaten nicht stationär sind, verwenden Sie das PACF-Diagramm der differenzierten Reihe, um nach geeigneten Begriffen für das ARIMA-Modell zu suchen.
In diesen Ergebnissen zeigen die Daten einen zunehmenden Trend zum Zeitreihendiagramm. Die erste Verzögerung im ACF-Diagramm zeigt eine große Spitze, die die Signifikanzgrenze von 5% überschreitet und dann sehr langsam abnimmt. Diese Muster weisen darauf hin, dass der Mittelwert der Daten nicht stationär ist.
Da Verkäufe keine Beziehung zu einem Prädiktor haben, der einen deterministischen Trend erklären würde, und der Analyst ein ARIMA-Modell verwenden möchte, um die Verkäufe zu prognostizieren, ist die Differenzierung der Daten eine vernünftige Möglichkeit, den Mittelwert der Serie stationär zu machen.
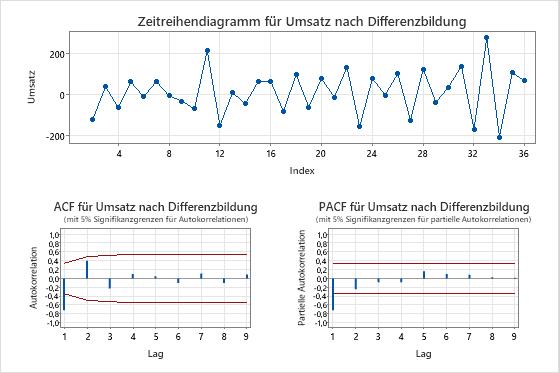
Plots der differenzierten Reihe
- Zeitreihendiagramm nach der Differenzierung
- Verwenden Sie das Zeitreihendiagramm der differenzierten Daten, um zu überprüfen, ob durch Differenzierung der Mittelwert der Daten stationär wird. Das Zeitreihendiagramm zeigt die Unterschiede zwischen aufeinanderfolgenden Beobachtungen. Daten mit stationärem Mittelwert folgen einem horizontalen Pfad im Zeitreihendiagramm.
- ACF-Diagramm und PACF-Diagramm nach Differenzierung
- Verwenden Sie die ACF der differenzierten Daten, um zu überprüfen, ob durch Differenzierung der Mittelwert der Daten stationär wird. Plots mit Spitzen, die schnell abnehmen, sind charakteristisch für stationäre Daten.
In diesen Ergebnissen zeigt das Zeitreihendiagramm, dass der Mittelwert und die Varianz der differenzierten Daten annähernd konstant sind. Die Daten sind anscheinend stationär.
Im ACF-Diagramm der differenzierten Daten befindet sich die einzige Spitze, die sich signifikant von 0 unterscheidet, bei Verzögerung 1. Dieses Muster deutet auch darauf hin, dass die Daten stationär sind.