Ein Marketinganalyst möchte ein ARIMA-Modell verwenden, um kurzfristige Prognosen für den Verkauf eines Shampoo-Produkts zu erstellen. Der Analyst sammelt Umsatzdaten aus den vergangenen drei Jahren. In einem Zeitreihendiagramm sieht der Analyst, dass die Daten höher tendieren. Dieses Muster zeigt an, dass der Mittelwert der Daten nicht stationär ist. Der Analyst führt einen erweiterten Dickey-Fuller-Test durch, um die Reihenfolge der nicht-saisonalen Differenzierung zu bestimmen, die in das ARIMA-Modell aufgenommen werden soll. Weitere Informationen zu ARIMA-Modell finden Sie unter Übersicht über ARIMA.
- Öffnen Sie die Beispieldaten VerkaufShampoo.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Datenreihe den Wert Umsatz ein.
- Wählen Sie OK aus.
Interpretieren der Ergebnisse
In diesen Ergebnissen ist der Teststatistik 2,29045 und somit größer als dem kritischen Wert von ungefähr -2,96053. Da die Ergebnisse die Nullhypothese, dass die Daten nicht stationär sind, nicht ablehnen, besteht die Empfehlung des Tests darin, die Differenzierung erster Ordnung in Betracht zu ziehen, um die Daten stationär zu machen.
Methode
| Maximale Lag-Ordnung für Terme im Regressionsmodell | 9 |
|---|---|
| Kriterium für Auswahl der Lag-Ordnung | Minimales AIC |
| Zusätzliche Terme | Konstante |
| Ausgewählte Lag-Ordnung | 4 |
| Verwendete Zeilen | 36 |
Erweiterter Dickey-Fuller-Test
| Nullhypothese: | Daten sind nicht stationär |
|---|---|
| Alternativhypothese: | Daten sind stationär |
| Teststatistik | p-Wert | Empfehlung |
|---|---|---|
| 2,29045 | 0,999 | Teststatistik > kritischer Wert von -2,96053. |
| Signifikanzniveau = 0,05 | ||
| Nullhypothese nicht zurückweisen. | ||
| Erwägen Sie eine Differenzbildung, um die Daten stationär zu machen. |
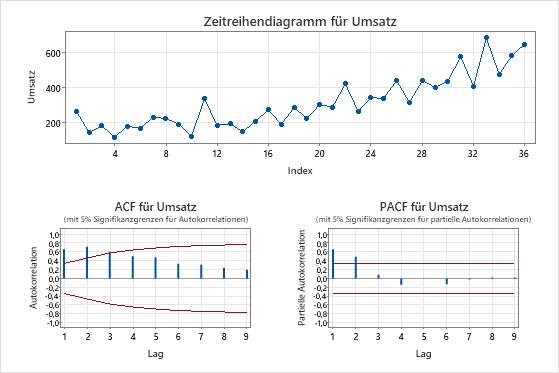
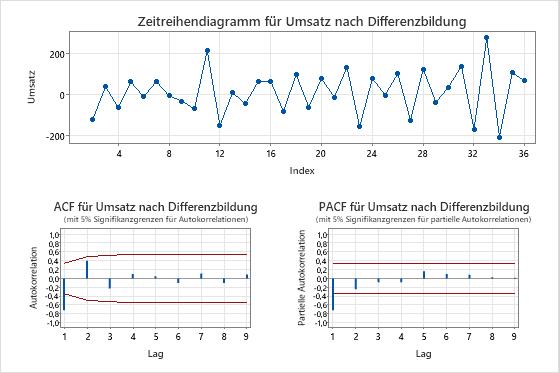
Die Zeitreihendiagramme zeigen das Ergebnis der Differenzierung. In diesen Ergebnissen zeigt das Zeitreihendiagramm der Originaldaten einen klaren Trend. Das Zeitreihendiagramm der differenzierten Daten zeigt die Unterschiede zwischen aufeinanderfolgenden Werten. Die differenzierten Daten erscheinen stationär, da die Punkte einem horizontalen Pfad ohne offensichtliche Muster in der Variation folgen.
Die ACF-Diagramme zeigen auch den Effekt der Differenzierung. In diesen Ergebnissen zeigt das ACF-Diagramm der Originaldaten langsam verringerte Spitzen über Lags hinweg. Dieses Muster zeigt an, dass die Daten nicht stationär sind. Im ACF-Diagramm der differenzierten Daten befindet sich die einzige Spitze, die sich signifikant von 0 unterscheidet, bei Verzögerung 1.
In diesen Ergebnissen bestätigen die Zeitreihendiagramme und die ACF-Diagramme die Testergebnisse. Daher ist es ein vernünftiger Ansatz, die Daten zu differenzieren und dann ein autoregressives und gleitendes Durchschnittsmodell anzupassen, um Prognosen zu erstellen.