In diesem Thema
Koeffizienten
Die Koeffizienten werden anhand eines iterativen Algorithmus geschätzt, der Schätzwerte der kleinsten Quadrate berechnet. Bei jeder Iteration werden die rückwärts gerichteten Prognosen und SSE berechnet. Weitere Informationen finden Sie in Box und Jenkins 1.
Der ARIMA-Algorithmus basiert auf der Anpassungsroutine im TSERIES-Programmpaket, das von Professor William Q. Meeker, Jr., an der Iowa State University geschrieben wurde2. Wir danken Professor Meeker für seine Hilfe bei der Anpassung seiner Routine an Minitab.
Rückwärts gerichtete Prognosen
Rückwärts gerichtete Prognosen werden anhand des angegebenen Modells und der Parameterschätzungen der aktuellen Iteration berechnet. Weitere Informationen finden Sie in Cryer3.
SSE
Formel
Notation
| Begriff | Beschreibung |
|---|---|
| n | Gesamtzahl der Beobachtungen |
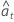 | Residuen unter Verwendung der Parameterschätzungen dieser Iteration, einschließlich rückwärts gerichteter Prognosen |
SS für Residuen
Formel
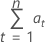
Notation
| Begriff | Beschreibung |
|---|---|
| n | Gesamtzahl der Beobachtungen |
| at | Residuen unter Verwendung der endgültigen Parameterschätzungen, ausgenommen rückwärts gerichtete Prognosen |
DF für Residuen
Formel
Für ein Modell mit konstantem Term:
(n – d) – p – q – 1
Für ein Modell ohne konstanten Term:
(n – d) – p – q
Notation
| Begriff | Beschreibung |
|---|---|
| n | Gesamtzahl der Beobachtungen |
| d | Anzahl der Differenzen |
| p | Anzahl der in das Modell eingebundenen Parameter für die Autoregression |
| q | Anzahl der in das Modell eingebundenen Parameter für den gleitenden Durchschnitt |
MS für Residuen
Formel
SS/DF
Chi-Quadrat-Statistik
Formel
Notation
| Begriff | Beschreibung |
|---|---|
| n | Gesamtzahl der Beobachtungen |
| d | Anzahl der Differenzen |
| K | 12, 24, 36, 48 |
| k | Lag |
 | Autokorrelation der Residuen für das k-te Lag |
DF für Chi-Quadrat-Statistik
Formel
Für ein Modell mit konstantem Term:
K – p – q – 1
Für ein Modell ohne konstanten Term:
K – p – q
Notation
| Begriff | Beschreibung |
|---|---|
| K | 12, 24, 36, 48 |
| p | Anzahl der in das Modell eingebundenen Parameter für die Autoregression |
| q | Anzahl der in das Modell eingebundenen Parameter für den gleitenden Durchschnitt |
p-Wert für Chi-Quadrat-Statistik
Formel
P(X < χ2)
Notation
| Begriff | Beschreibung |
|---|---|
| X | x2(DF)-verteilt |
Prognosen
Formel
Die Prognosen werden rekursiv anhand des Modells und der Parameterschätzungen berechnet. Wenn z. B. ein ARIMA-Modell mit einem autoregressiven Term (AR(1)) und einem Term für die saisonale Differenzbildung mit einer saisonalen Periode von 12 angepasst wird, wird dieses Modell angepasst:
Yt – Yt–12 = γ + Φ(Yt–1 – Yt–12–1)
Zum Schätzen von 
, der ersten Prognose, wobei k der Ursprung ist, wird diese Gleichung ausgewertet:
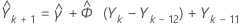
Anschließend wird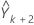 
auf dieselbe Weise ermittelt usw.
Zum Berechnen des 95%-Prognoseintervalls müssen zuerst die Gewichtungen berechnet werden.
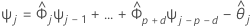
Dabei gilt: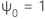 
, 
für j < 0, und 
für j > q.
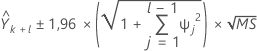
Notation
| Begriff | Beschreibung |
|---|---|
| Yt | tatsächlicher Wert zum Zeitpunkt t |
| Φ | autoregressiver Term |
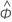 | geschätzter autoregressiver Term |
| γ | konstanter Term |
| d | Anzahl der Differenzen |
| p | Anzahl der autoregressiven Parameter |
| q | Anzahl der Parameter für den gleitenden Durchschnitt |
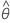 | geschätzter Term für den gleitenden Durchschnitt |
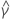 | geschätzter konstanter Term |
| MS | mittleres Fehlerquadrat |
