In diesem Thema
Zeitreihendiagramm
Zeitreihendiagramme stellen Daten in chronologischer Reihenfolge dar. Wenn Sie Prognosen erstellen, werden im Diagramm zusätzlich zu den Prognosen die entsprechenden 95%-Konfidenzintervalle gezeigt.
Interpretation
- Ermitteln Sie, ob die Daten im Verlauf der Zeit unterschiedlich gestreut sind. Wenn unterschiedliche Streuungsgrade vorhanden sind, müssen Sie die Daten so transformieren, dass die Varianz konstant ist.
- Ermitteln Sie, ob die Daten um einen konstanten Mittelwert zentriert sind. Wenn der Mittelwert nicht konstant ist, müssen Sie möglicherweise Differenzen der Daten bilden, um einen konstanten Mittelwert zu erhalten.
ACF der Residuen
Das Diagramm zeigt die Autokorrelationsfunktion der Residuen. Bei der Autokorrelationsfunktion handelt es sich um ein Maß für die Korrelation zwischen den um k Zeiteinheiten auseinander liegenden Beobachtungen einer Zeitreihe (yt und yt–k).
Interpretation
Verwenden Sie die Autokorrelationsfunktion der Residuen, um zu ermitteln, ob das Modell die Annahme erfüllt, dass die Residuen unabhängig sind. Wenn sich die Annahme nicht bestätigt, ist das Modell möglicherweise nicht an die Daten angepasst, und Sie sollten beim Interpretieren der Ergebnisse vorsichtig sein. Wenn keine signifikanten Korrelationen vorhanden sind, können Sie schlussfolgern, dass die Residuen unabhängig sind. Es kann jedoch sein, dass Sie ein oder zwei signifikante Korrelationen bei Lags höherer Ordnung feststellen, bei denen es sich nicht um saisonale Lags handelt. Diese Lags sind in der Regel auf Zufallsfehler zurückzuführen und kein Anzeichen dafür, dass die Annahme nicht zutrifft. In diesem Fall können Sie also ebenfalls schlussfolgern, dass die Residuen unabhängig sind.
PACF der Residuen
Die partielle Autokorrelationsfunktion ist ein Maß für die Korrelation zwischen den um k Zeiteinheiten auseinander liegenden Beobachtungen einer Zeitreihe (yt und yt–k) nach Korrektur für das Vorhandensein aller andere Terme mit geringerem Lag (yt–1, yt–2, ..., yt-k–1).
Interpretation
Verwenden Sie die partielle Autokorrelationsfunktion der Residuen, um zu ermitteln, ob das Modell die Annahme erfüllt, dass die Residuen unabhängig sind. Wenn sich die Annahme nicht bestätigt, ist das Modell möglicherweise nicht an die Daten angepasst, und Sie sollten beim Interpretieren der Ergebnisse vorsichtig sein. Wenn keine signifikanten Korrelationen vorhanden sind, können Sie schlussfolgern, dass die Residuen unabhängig sind.
Histogramm der Residuen
Das Histogramm der Residuen zeigt die Verteilung der Residuen für alle Beobachtungen. Wenn das Modell gut an die Daten angepasst ist, sollten die Residuen zufällig ausfallen und den Mittelwert 0 aufweisen. Das Histogramm sollte also annähernd symmetrisch um 0 sein.
Wahrscheinlichkeitsnetz (Normal) für Residuen
Das Wahrscheinlichkeitsnetz (Normal) für Residuen stellt die Residuen im Vergleich zu den Werten dar, die bei Vorliegen einer Normalverteilung erwartet würden.
Interpretation
Prüfen Sie mit Hilfe des Wahrscheinlichkeitsnetzes (Normal) für Residuen, ob die Residuen normalverteilt sind. Für diese Analyse sind jedoch keine normalverteilten Residuen erforderlich.
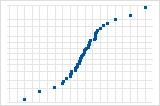
Die S-Kurve deutet auf eine Verteilung mit langen Randbereichen hin.
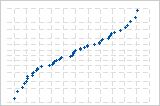
Die invertierte S-Kurve deutet auf eine Verteilung mit kurzen Randbereichen hin.
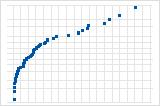
Eine Abwärtskurve deutet auf eine rechtsschiefe Verteilung hin.
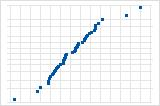
Wenige Punkte, die abseits der Linie liegen, deuten auf eine Verteilung mit Ausreißern hin.
Residuen vs. Anpassungen
Im Diagramm der Residuen im Vergleich mit den Anpassungen werden die Residuen auf der y-Achse und die angepassten Werte auf der x-Achse abgetragen.
Interpretation
Ermitteln Sie anhand des Diagramms „Residuen vs. Anpassungen“, ob die Residuen unverzerrt sind und eine konstante Varianz aufweisen. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte | Nicht konstante Varianz |
| Krümmung | Ein fehlender Term höherer Ordnung |
| Ein weit von null entfernt liegender Punkt | Ein Ausreißer |
Wenn Sie in den Residuen eine nicht konstante Varianz oder Muster erkennen, ist Ihre Prognose möglicherweise nicht genau.
Residuen vs. Reihenfolge
Das Diagramm der Residuen vs. Reihenfolge zeigt die Residuen in der Reihenfolge an, in der die Daten erfasst wurden.
Interpretation
Ermitteln Sie anhand des Diagramms der Residuen vs. Reihenfolge, wie genau die angepassten Werte im Vergleich zu den im Beobachtungszeitraum beobachteten Werten sind. Muster in den Punkten können darauf hinweisen, dass das Modell nicht an die Daten angepasst ist. Im Idealfall sollten die Residuen im Diagramm zufällig um die Mittellinie angeordnet sein.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Ein einheitlicher Langfrist-Trend | Das Modell ist nicht an die Daten angepasst. |
| Ein Kurzfrist-Trend | Eine Verschiebung oder Änderung im Muster |
| Ein weit von den anderen Punkten entfernt liegender Punkt | Ein Ausreißer |
| Ein Sprung in den Punkten | Das zugrunde liegende Muster der Daten hat sich geändert. |
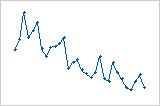
Die Residuen nehmen systematisch mit den von links nach rechts zunehmenden Beobachtungen ab.
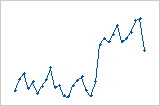
Es tritt eine sprunghafte Änderung in den Werten der Residuen von klein (links) nach groß (rechts) auf.
Residuen vs. Variablen
Das Diagramm der Residuen vs. Variablen zeigt die Residuen im Vergleich mit einer anderen Variablen.
Interpretation
Mit diesem Diagramm können Sie ermitteln, ob sich die Variable systematisch auf die Antwortvariable auswirkt. Wenn in den Residuen Muster vorhanden sind, besteht eine Assoziation zwischen den anderen Variablen und der Antwortvariablen. Sie können diese Informationen als Grundlage für weitere Untersuchungen verwenden.
